5) по результатам обработки выборочных данных выдвинуть гипотезу о нормальном распределении генеральной совокупности, например, по виду гистограммы, и выполнить ее проверку, используя правило «
»;
6) построить кривую нормального распределения по опытным данным, приняв в формуле Гаусса математическое ожидание 
и 
;
7) найти доверительный интервал для генеральной средней 
. Принять уровень значимости 
Решение:
1) Выполним ранжирование выборочных данных:
Таким образом, имеем: 
.
2) Для построения равноинтервального вариационного ряда:
– найдем по формуле Стерджеса число интервалов (обратите внимание, что число интервалов – целое число) 
: 
;
– вычислим ширину интервала 
;
– вычисления границ интервалов и пр. выполним в таблице:
Границы интервалов | [63;69,83) | [69,83;76,66) | [76,66;83,49) | [83,49;90,32 | 90,32;97,15) | [97,15;104] |
|
Число попаданий в интервал, | 2 | 4 | 9 | 15 | 8 | 2 | 40 |
Относительная частота, | 0,05 | 0,1 | 0,225 | 0,375 | 0,2 | 0,05 | 1 1 |
Плотность относительной частоты, | 0,007 | 0,015 | 0,033 | 0,055 | 0,029 | 0,007 | – – |
Середина интервала, | 66,415 | 73,245 | 80,085 | 86,905 | 93,735 | 100,575 | – – |
3) Гистограмма распределения рис 6.
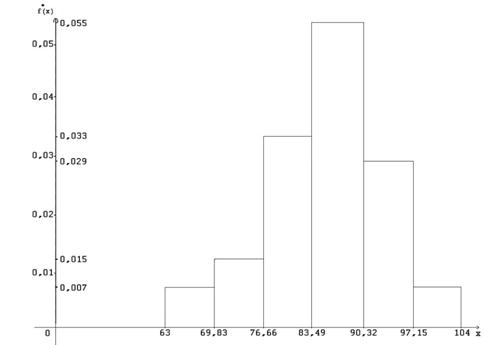
Рис 6. Гистограмма распределения величины Х
3) вычислим основные числовые характеристики выборки:
– моду: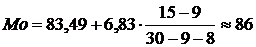 
;
– медиану: 
;
– выборочную среднюю:
– 
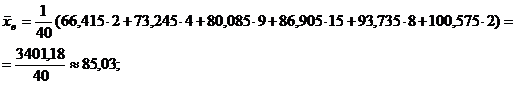
– выборочную дисперсию:
– 
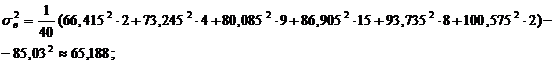
– выборочное среднеквадратическое отклонение:
– 
– коэффициент вариации: 
,
значение коэффициента вариации означает, что разброс значений признака слабый.
5) Вид гистограммы позволяет выдвинуть гипотезу, о том, что данная выборка принадлежит нормально распределенной генеральной совокупности.
Для проверки выдвинутой гипотезы воспользуемся правилом «трех сигм», согласно которому при нормальном распределении признака все его значения принадлежат интервалу (
), а значит 
.
Проверим это:
;
.
Таким образом, при уровне значимости 
принимаем выдвинутую гипотезу, т. е. выборка принадлежит нормально распределенной генеральной совокупности.
6) Для построения кривой нормального распределения по опытным данным примем в формуле Гаусса математическое ожидание и .
Кривая распределения представляет собой график функции плотности вероятности.
Плотность вероятности нормального распределения вычисляется по формуле Гаусса:
,
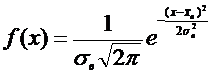где 
– значение варианты, 
– значение выборочной средней, 
– значение выборочной дисперсии, 
– выборочное среднеквадратическое отклонение.
Для построения кривой Гаусса достаточно вычислить координаты 7 точек:
;
;
;
.
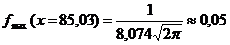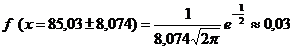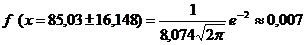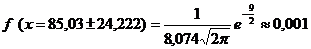Построим график кривой Гаусса на фоне гистограммы (рис 7).
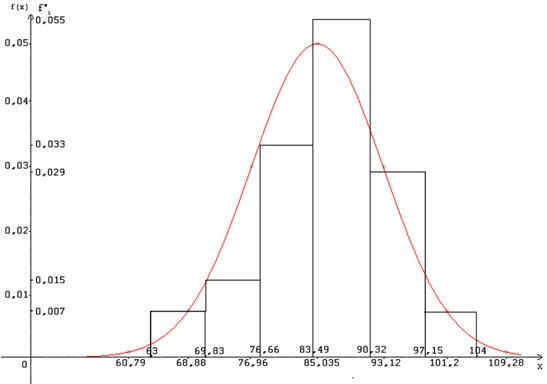
Рис 7. Кривая Гаусса на фоне гистограммы, построенные по исходным данным
7) найдем доверительный интервал для генеральной средней. Для этого вычислим:
;
;
,
здесь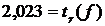 
найдено по заданным значениям 
и 
(или 
по таблице Приложения 6. Таким образом, получаем, что
или
при уровне значимости .
Т. к. измерения величины Х проводились с точностью до целых, то окончательный результат записываем с точностью до 0.1
КОРЕЛЯЦИОННО-РЕГРЕССИОННЫЙ АНАЛИЗ
Функциональная зависимость между двумя переменными величинами характеризуется тем, что каждому значению одной из них соответствует вполне определенное значение другой. Например, между радиусом круга r и его площадью S существует функциональная зависимость, которая выражается формулой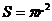 
. Однако, на практике часто встречаются и такие виды связей между величинами, которые нельзя отнести к функциональной зависимости. Корреляционная связь не является точной зависимостью одного признака от другого. Еще Гиппократ в 6 веке до нашей эры обратил внимание на наличие связи между телосложением и темпераментом людей, между строением тела и предрасположенностью к тем или иным заболеваниям. Масса тела, рост, пульс, ЧДД связаны с возрастом детей; изменение диуреза обусловлены изменениями клубочковой фильтрации и канальцевой реадбсорбции; пульс меняется при изменениях АД и температуры тела. К примеру, существует корреляционная связь между ростом и весом взрослых мужчин. Одному значению переменной Y(рост, см) соответствует множество значений переменной X(вес, кг), и, наоборот, мужчины с весом 75 кг могут быть самого разного роста. Тем не менее, в целом более высокие мужчины имеют больший вес.
Корреляционный анализ решает задачи обнаружения связей между варьирующими признаками и установления характера этих связей.
Корреляционная связь не является точной зависимостью одного признака от другого – она может иметь различную степень: от полной независимости до очень сильной связи. Кроме того, характер связи между признаками может быть различен по форме и направлению. По форме корреляции может быть прямолинейной и криволинейной, по направлению – прямой (или положительной) и обратной (или отрицательной). Степень корреляции определяется различными показателями, введенными для установления силы связи между количественными признаками. Такими показателями являются коэффициент парной корреляции rxy, корреляционное отношение 
, тетрахорический, полилихорический показатели связи, частный и множественный коэффициенты корреляции.
|
Из за большого объема этот материал размещен на нескольких страницах:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 |
Основные порталы (построено редакторами)