3) Событие 
произошло. Условную вероятность того, что при этом сработал третий датчик, (событие 
) найдем по формуле Байеса:
, или
.
Ответ: 1) вероятность того, что по достижении предельно допустимой концентрации пыли сигнализация сработает, равна 
; 2) вероятность того, что сигнализацию при этом включил третий датчик, равна 
.
Задача 4. Вероятность заражения желудочно-кишечными заболеваниями при однократном приеме внутрь 250 мл не кипяченой речной воды составляет 0,1. Какова вероятность того, что из группы туристов, насчитывающей 6 человек, заболеет хотя бы один, если все они выпили по 250 мл не кипяченой речной воды?
Решение: События – заражение желудочно-кишечными заболеваниями относятся к повторным независимым испытаниям. Вероятность того, что некоторое событие произойдет ровно 
раз в 
испытаниях, вычисляется по формуле Бернулли:
.
По условию: 
, 
, 
(событие – «хотя бы один» – означает «один и более»), т. е.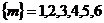 
.
Известно, что сумма вероятностей событий, составляющих полную систему, равна 1, т. е. 
. Для данного случая имеем: 
или 
,
тогда получаем, что 
.
Вычислим 
:
.
Ответ: вероятность того, что из группы туристов, насчитывающей 6 человек, заболеет хотя бы один, равна 
.
Задача 5. Какова вероятность того, что в партии таблеток, насчитывающей 10000 штук, 1) не более 20 окажутся нестандартными, если вероятность того, что отдельная таблетка окажется нестандартной, составляет 0,0012? 2) ровно 12 штук окажутся нестандартными?
Решение: События – нестандартная таблетка – относятся к повторным независимым испытаниям.
Число испытаний (
) в данном случае велико, поэтому использование формулы Бернулли для нахождения вероятности 
приводит к вычислительным трудностям.
1) Для ответа на первый вопрос используем формулу, позволяющую приближённо определять вероятность 
, с которой происходит событие .
По условию: , 
, 
, 
, 
.
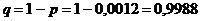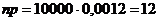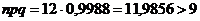Анализ условия показывает, что 
, значит, для вычисления вероятности 
используем интегральную теорему Лапласа:
,
здесь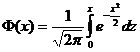 
– стандартный интеграл вероятностей (функция Лапласа), 
, 
, причем 
. Таким образом, получаем:
.
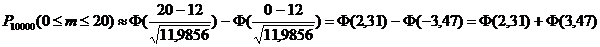По таблице значений функции 
находим (Приложение 2), что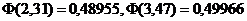 
, тогда вероятность
.
2) Для ответа на второй вопрос используем формулу, позволяющую приближённо определять вероятность , с которой происходит событие :
, где 
, 
(локальная теорема Лапласа).
По условию: , , , , 
, 
.
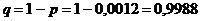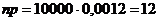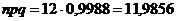Вычисляем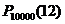 
:
.
По таблице значений функции 
находим (Приложение 1), что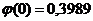 
.
Тогда 
.
Ответ: 1) вероятность того, что в партии таблеток из 10000 штук, не более 20 окажутся нестандартными, равна 
; 2) вероятность того, что в партии таблеток из 10000 штук, ровно 12 окажутся нестандартными, равна 
.
Задача 6. Среднее число самолетов, прибывших в аэропорт за 1 минуту, равно 3. Найти вероятность того, что за 2 минуты прибудут: а) не менее 3-х самолетов; б) не более 2; в) 4 самолета.
Решение: События – прибытия самолетов в аэропорт – представляют собой простейший поток событий.
Вероятность появления событий простейшего потока за время длительностью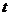 
определяется формулой Пуассона: 
, где
– интенсивность простейшего потока, или среднее число событий, появляющихся в единицу времени.
По условию: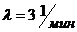 
, 
:
а) 
, т. е. 
. Для полной системы событий имеем: .
Или в данном случае: 
. Тогда интересующая нас вероятность 
.
Вычисляем: 
, 
, 
, 
;
|
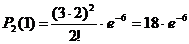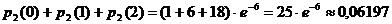
Из за большого объема этот материал размещен на нескольких страницах:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 |
Основные порталы (построено редакторами)