Определение. Число всех объектов, составляющих генеральную совокупность, называется ее объёмом и обозначается 
.
Определение. Конечный набор объектов, случайным образом отобранный из генеральной совокупности, называется выборочной совокупностью, или выборкой.
Определение. Число объектов выборки называется ее объёмом и обозначается 
.
Для того, чтобы по выборке можно было сделать правильные выводы обо всей генеральной совокупности, она должна быть репрезентативной. Это значит, что все пропорции генеральной совокупности должны быть представлены в выборке. Репрезентативность выборки обеспечивается случайностью отбора. Это означает, что любой объект выборки отобран случайно, при этом все объекты имеют одинаковую вероятность попасть в выборку. Иными словами выборка должна давать обоснованное представление о генеральной совокупности. Для обеспечения репрезентативности выборка должна быть достаточно объемной с тем, чтобы охватывать всю генеральную совокупность, и производится беспристрастно по отношению к отдельным ее частям.
Статистическое распределение выборки
При систематизации данных выборочных обследований используются статистические дискретные и интервальные ряды распределения.
Полученные результаты исследований представляют собой множество беспорядочных данных. Для изучения их подвергают обработке. Изучение структуры совокупности достигается построением рядов распределения, характеризующих распределение единиц совокупности по одному признаку. Распределение единиц совокупности по количественному признаку называют вариационным рядом. Ряд может быть построен как по дискретному, так и по непрерывному признаку.
Определение. Дискретным называется признак, который может принимать определенные значения из конечного набора таких значений, выражаемых, как правило, целыми числами, например, число детей в детском саду.
Определение. Непрерывный признак может принимать любые промежуточные значения. Как правило, при построении вариационных рядов по непрерывному признаку последний указывается в виде интервалов «от и до», и ряд называется интервальным.
Выделяют статистические дискретные и интервальные ряды распределения.
Статистический дискретный ряд распределения
Для того чтобы построить ряд распределения необходимо иметь выборку объема . В данной выборке наименьшее значение 
, признака встречается 
раз, следующее по величине 
встречается 
раз, 
– 
раз.
Каждый элемент выборки обозначается 
и называется вариантой. Число наблюдений варианты 
в выборке называется частотой встречаемости данной варианты. Последовательность вариант, записанных в определенном порядке, называется вариационным рядом.
Определение. Статистическое распределение – это совокупность вариант и соответствующих им частот . Сумма всех частот равна объему выборки: 
.
Определение. Относительными частотами называются отношения вида: 
, 
, …, 
, …, 
, причем 
.
Дискретное распределение частот записывается в виде таблицы, первая строка которой содержит все варианты , перечисленные по возрастанию, а вторая строка содержит соответствующие вариантам частоты встречаемости .
|
|
|
|
|
|
|
|
|
|
Замечание. Вторая строка в таблице может содержать соответствующие вариантам относительные частоты 
.
Для графического изображения такого ряда на координатной плоскости откладывают точки 
и соединяют их отрезками прямых. Получают наглядное представление статистического распределения – ломаную линию, называемую полигоном частот рис 4.
Рис 4. Полигон частот
Статистический интервальный ряд распределения
Определение. Интервальным вариационным рядом называется упорядоченная совокупность интервалов варьирования значений случайной величины с соответствующими частотами (или долями) попаданий в каждый из них значений величины.
Число интервалов 
находится по формуле Стерджеса (если объем большой выборки не более 100):
.
Ширина интервала находится по формуле:
,
где –число интервалов, 
– максимальное значение варианты и 
– минимальное значение варианты.
Для наглядного представления статистического интервального ряда распределения строится гистограмма.
На оси Ox откладывают частичные интервалы длиной 
. На каждом частичном интервале строят прямоугольник с основанием , равным длине частичного интервала, и высотой 
(или 
), равной частному от деления частоты интервала (относительной частоты) на длину интервала. Частоту (относительную частоту), приходящуюся на единицу интервала, называют плотностью частоты (относительной частоты). Площадь i – го частичного прямоугольника равна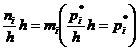 
. Полученную таким образом ступенчатую фигуру, состоящую из прямоугольников, называют гистограммой. Площадь гистограммы равна сумме всех частот (относительных частот), т. е. объему выборки (единице).
Интервалы, x |
|
|
|
|
Плотность частоты, |
|
|
|
|
Аналогичную таблицу можно образовать, заменяя в нижней строке плотность частоты на плотность относительной частоты .
|
Из за большого объема этот материал размещен на нескольких страницах:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 |
Основные порталы (построено редакторами)