Гистограмма плотности частот состоит из прямоугольников с основаниями  , высота которых равна
, высота которых равна ![]() рис 5.
рис 5.
Рис 5. Гистограмма плотности частот
Выборочные характеристики
Характеристики положения
Определение. Выборочной средней называется среднее арифметическое значение вариант статистического ряда. Вычисляется по формуле:
![]() .
.
Определение. Модой ![]() называется наиболее часто встречающая в ряду распределения варианта. Она дает представление о центре распределения вариационного ряда.
называется наиболее часто встречающая в ряду распределения варианта. Она дает представление о центре распределения вариационного ряда.
В дискретном вариационном ряду мода – варианта, встречающая с наибольшей частотой.
В интервальном ряду мода вычисляется по формуле:
![]() ,
,
где ![]() – нижняя граница модального интервала, т. е. интервала с наибольшей частотой встречаемости
– нижняя граница модального интервала, т. е. интервала с наибольшей частотой встречаемости ![]() ;
; ![]() – частота модального интервала;
– частота модального интервала; ![]() – частота интервала, предшествующего модальному;
– частота интервала, предшествующего модальному; ![]() – частота интервала, следующего за модальным;
– частота интервала, следующего за модальным; ![]() – ширина модального интервала.
– ширина модального интервала.
Определение. Медианой ![]() называется серединная варианта, центральный член ранжированного ряда. Если вариант в ряду четное количество, то медиана равна полусумме двух вариант, находящихся в середине ранжированного ряда.
называется серединная варианта, центральный член ранжированного ряда. Если вариант в ряду четное количество, то медиана равна полусумме двух вариант, находящихся в середине ранжированного ряда.
В интервальном ряду медиана вычисляется по формуле:
![]()
где ![]() – нижняя граница медианного интервала,
– нижняя граница медианного интервала, ![]() – частота медианного интервала;
– частота медианного интервала; ![]() – частота интервала, предшествующего медианному;
– частота интервала, предшествующего медианному; ![]() – сумма частот ряда,
– сумма частот ряда, ![]() – ширина медианного интервала.
– ширина медианного интервала.
Показатели рассеяния вариант
Выборочная дисперсия – среднее арифметическое квадратов отклонений вариант от их среднего значения.
![]()
Существующий недостаток дисперсии, которая является именованной величиной, – несоответствие ее размерности и размерности отдельных единиц числового ряда. Если варианты выражены в метрах, то дисперсия дает квадратные метры; если варианты в килограммах, то дисперсия дает квадрат этой меры, и т. д. Указанного недостатка лишено среднеквадратическое отклонение.
Выборочное среднеквадратическое отклонение представляет собой корень квадратный из дисперсии:
![]() .
.
Коэффициент вариации представляет собой процентное отношение среднеквадратического отклонения к среднему арифметическому:
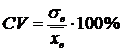 .
.
Коэффициент вариации позволяет оценивать вариабельность (разброс) признака в нормированных границах. Если его значение не превышает 10%, то можно говорить о слабом разбросе. Если коэффициент вариации находится в пределах 10-20%, разброс средний, если превышает 20%, то разброс вариант считают большим.
Точечная оценка параметров генеральной совокупности
Определение. Любая выборочная характеристика, используемая в качестве приближенного значения генеральной характеристики и получаемая вычислением одного числа (точки), называется точечной статистической оценкой.
При избрании способа получения точечных оценок учитывается, что они должны обладать свойствами состоятельности, несмещенности и эффективности.
Определение. Состоятельной оценкой называется точечная оценка, которая при неограниченном увеличении объема выборки приближается (сходится) к истинному значению оцениваемой генеральной характеристики. Выборочную среднюю можно считать состоятельной точечной оценкой генерального среднего.
Определение. Несмещенной оценкой называется точечная оценка, лишенная систематической ошибки.
Выборочная средняя ![]() – несмещенная оценка генеральной средней.
– несмещенная оценка генеральной средней.
Выборочная оценка дисперсии – смещенная оценка. Для определения генеральной дисперсии по выборочным данным используют формулу:
![]()
и получают смещенную точечную оценку генеральной дисперсии.
Для получения несмещенной точечной оценки генеральной дисперсии из выборочных данных используют формулу расчета исправленной дисперсии:
![]()
При больших объемах выборки смещенная и несмещенная (исправленная) дисперсия отличаются незначительно. На практике пользуются исправленной дисперсией, если число наблюдений не превышает 30 вариант 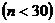 , поскольку при большем числе наблюдений влияние становится несущественным.
, поскольку при большем числе наблюдений влияние становится несущественным.
Определение. Эффективной оценкой называют такую точечную оценку, которая гарантирует наименьшее отклонение выборочной оценки от такой же оценки генеральной совокупности.
В расчетах используются исправленное среднеквадратическое отклонение (стандартное отклонение):
![]()
и ошибка выборочной средней (стандартная ошибка среднего или ошибка репрезентативности) ![]()
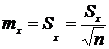 .
.
Интервальные оценки параметров генеральной совокупности
Определение. Интервальной оценкой называется числовой интервал, который определяется двумя числами – границами интервала, содержащего неизвестный параметр генеральной совокупности.
Определение. Доверительным интервалом называется интервал, в котором с той или иной заранее заданной вероятностью находится неизвестный параметр генеральной совокупности.
Доверительная вероятность ![]() – вероятность, что событие вероятности
– вероятность, что событие вероятности ![]() можно считать невозможным,
можно считать невозможным, ![]() – уровень значимости. В качестве доверительных вероятностей используют вероятности, близкие к 1 (например, 0,95; 0,99; 0,999).
– уровень значимости. В качестве доверительных вероятностей используют вероятности, близкие к 1 (например, 0,95; 0,99; 0,999).
Для малых выборок ![]() нормально распределенного количественного признака Х доверительный интервал имеет вид:
нормально распределенного количественного признака Х доверительный интервал имеет вид:
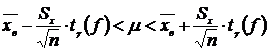 ,
,
где ![]() – коэффициент Стьюдента, значение которого определяется величиной доверительной вероятности
– коэффициент Стьюдента, значение которого определяется величиной доверительной вероятности ![]() и числом степеней свободы
и числом степеней свободы ![]() (Приложение 4).
(Приложение 4).
Для больших выборок ![]() нормально распределенного количественного признака Х доверительный интервал имеет вид:
нормально распределенного количественного признака Х доверительный интервал имеет вид:
![]() ,
,
где ![]() – коэффициент Стьюдента, значение которого определяется величиной доверительной вероятности
– коэффициент Стьюдента, значение которого определяется величиной доверительной вероятности ![]() и числом степеней свободы
и числом степеней свободы ![]() (Приложение 4).
(Приложение 4).
Пример решения задач:
Задача. Пусть дана последовательность значений некоторого признака: 63, 77, 68, 77, 77, 71, 104, 102, 93, 83, 81, 72, 74, 74, 79, 79, 82, 82, 84, 84, 85, 85, 84, 85, 85, 87, 87, 86, 95, 95, 86, 86, 88, 88, 88, 91,91, 91, 96, 96. Выполните статистическую обработку данных по следующей схеме:
1) выполнить ранжирование признака и составить безинтервальный вариационный ряд распределения, выбрав ![]() его значений (согласно своему варианту);
его значений (согласно своему варианту);
2) составить равноинтервальный вариационный ряд, разбив всю вариацию на ![]() интервалов;
интервалов;
3) построить гистограмму распределения;
4) найти числовые характеристики выборочной совокупности (моду, медиану, выборочную среднюю, выборочную дисперсию, коэффициент вариации);

|
Из за большого объема этот материал размещен на нескольких страницах:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 |
 Основные порталы (построено редакторами)
Основные порталы (построено редакторами)

