Обложка тетради заполняется по следующей форме:
Контрольная работа по дисциплине
«Теория вероятностей и математическая статистика»
Вариант №_____
Студента 2 курса
заочного отделения направления подготовки Менеджмент
Волгоградского государственного медицинского университета
Фамилия, имя, отчество (полностью)
№ зачётной книжки ____________
Домашний адрес: _________________________
Дата отправки ________
Прорецензированную зачтённую контрольную работу вместе со всеми исправлениями и дополнениями, сделанными по требованию рецензента, студент должен представить при сдаче экзамена. В противном случае студент к сдаче экзамена не допускается.
При сдаче экзамена студент должен показать:
а) чёткое знание математических определений и формул, предусмотренных программой, и умение обосновать их (доказательство теорем, вывод формул);
б) умение точно и сжато выражать математическую мысль (в особенности при формулировке теорем и определений);
в) умение применять приобретенные навыки по дисциплине к решению задач (при оценке решения учитывается, насколько быстро приводят к цели применяемые средства, и в какой мере автор решения умеет его обосновывать).
2 Основные теоретические вопросы курса
1. Множество элементарных событий. Случайные события и их классификация. Полная группа событий. Частота событий и ее свойство статистической устойчивости. Классическое и статистическое определения вероятности случайного события. Аксиомы теории вероятностей и следствие из них.
2. Основные теоремы теории вероятностей.
3. Случайная величина как математическая модель вероятностного явления. Дискретные и непрерывные случайные величины. Закон распределения дискретной случайной величины, многоугольник распределения. Функции распределения и функции плотности распределения вероятностей случайных величин и их свойства.
4. Распределение Бернулли, распределение Пуассона. Локальная и интегральная теоремы Муавра-Лапласса.
5. Числовые характеристики дискретной случайной величины и их свойства.
6. Функция распределения и плотность вероятности НСВ. Числовые характеристики непрерывной случайной величины. Нормальный закон распределения. Вероятность попадания значения нормально распределенной СВ в заданный интервал. Правило «трех сигм».
7. Неравенство Чебышева. Дисперсионная и корреляционная матрицы случайного вектора. Ковариация и коэффициент корреляции двух случайных величин.
8. Предельные теоремы в теории вероятностей. Закон больших чисел, теорема Чебышева. Центральная предельная теорема для одинаково распределенных независимых случайных величин, центральная теорема Муавра-Лапласа, как ее следствие.
9. Оценивание скорости сходимости частоты к вероятности в схеме независимых испытаний Бернулли, сравнение результатов использования неравенства Чебышева и интегральной теоремы Муавра-Лапласа.
11. Основные задачи математической статистики. Генеральная и выборочная совокупности. Репрезентативность выборки. Статистическое распределение выборки, дискретные и интервальные вариационные ряды, полигон, гистограмма. Эмпирическая функция распределения вероятностей.
12. Оценки числовых характеристик распределения по данным распределения. Точечные оценки параметров распределения. Генеральная средняя и выборочная средняя. Генеральная дисперсия и выборочная дисперсия.
13. Несмещенная и смещенная оценки генеральной дисперсии: выборочная и исправленная выборочная дисперсии. Доверительный интервал и доверительная вероятность. Нахождение границ доверительного интервала для оценки математического ожидания нормально распределенной случайной величины по данным выборки малого объема. Распределение Стьюдента. Статистическая проверка статистических гипотез. Нулевая и конкурирующая гипотезы.
14. Критерии согласия, критерии однородности, критерии независимости, критерии значимости, знаковый анализ, ранговый анализ в задачах анализа данных.
15. Коэффициенты ранговой корреляции Спирмена и Кендалла, коэффициент конкордации.
16. Модели и методы непараметрической статистики.
17. Элементы дисперсионного и корреляционного анализов. Понятие кластер-анализа
18. Элементы теории временных (динамических) рядов.
19. Задачи оптимизации в здравоохранении (оптимизация планов обследования, перевозок и т. д.). Понятие о линейном программировании. Понятие о целевой функции.
ОСНОВЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ. СЛУЧАЙНЫЕ СОБЫТИЯ
Теория вероятностей – раздел математики, где изучаются закономерности случайных событий.
Теория вероятностей дает количественное измерение вероятностей случайных явлений и построение на этой основе математической модели наблюдаемых случайных эмпирических соотношений.
Испытание и событие
В природе и повседневной жизни часто приходится сталкиваться со случайными явлениями, т. е. с ситуациями, исход которых нельзя точно предвидеть. Процесс познания действительности в этом случае осуществляется в результате наблюдений или испытаний (экспериментов).
Определение. Под испытанием (наблюдением) понимается любой доступный частому повторению процесс, протекающий при реализации заданного комплекса условий.
Определение. Результат, или исход испытания называется событием.
Виды событий
Различают три вида событий: случайные, достоверные и невозможные.
Определение. Событие, которое при реализации заданного комплекса условий может произойти, а может и не произойти, называется случайным.
Определение. Событие, которое неизбежно происходит при каждой реализации заданного комплекса условий, называется достоверным.
Определение. Событие, которое заведомо не может произойти при реализации заданного комплекса условий, называется невозможным.
Виды случайных событий
Случайные события подразделяются на следующие виды: равновозможные, несовместные и совместные, зависимые и независимые.
Определение. Два или несколько случайных событий называются равновозможными, если условия их появления одинаковы и нет основания утверждать, что какое-либо из них в результате испытания имеет больше шансов осуществиться, чем другие.
Определение. События называются несовместными, если в результате испытания осуществление одного из них исключает осуществление остальных.
Определение. Два события называются совместными, если появление одного из них не исключает появления другого в одном и том же испытании.
Определение. Два события называются независимыми, если появление одного из них не влияет на шансы появления другого.
Определение. Два события называются зависимыми, если появление одного из них влияет на шансы появления другого.
Полная группа событий
Определение. Если в результате испытания обязательно осуществится одно и только одно из несовместных событий 
, то эти события называются полной группой событий.
Определение. Два несовместных события, образующие полную группу событий, называются противоположными.
Исходы испытания
Определение. Несовместные события, имеющие одинаковую возможность осуществиться, называются исходами испытания.
Определение. Исходы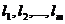 
называются благоприятными для события 
, если осуществление любого из исходов является вместе с тем осуществлением события .
Операции над событиями
Определение. Если при каждом осуществлении заданного комплекса условий, при котором происходит событие , происходит и событие 
, то говорят, что влечёт за собой , и обозначают символом 
или 
.
Определение. Если влечет за собой и в то же время влечёт за собой , т. е. события и оба наступают или оба не наступают, то говорят, что события и равносильны, и обозначают символом 
.
Определение. Событие, состоящее в наступлении обоих событий и , называется произведением (или пересечением) событий и , и обозначается символом 
или 
.
|
Из за большого объема этот материал размещен на нескольких страницах:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 |
Основные порталы (построено редакторами)