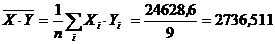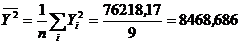; 
;
; 
;
Далее получаем: 
;
;
.
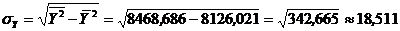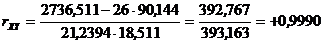Вывод 1: Полученное значение выборочного коэффициента парной корреляции 
показывает согласно шкале Чеддока, что в выборочной совокупности между признаками 
(растворимостью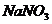 
) и 
(температурой раствора) обнаружена сильная положительная связь.
3) Проверим достоверность найденного значения . Для этого:
– вычислим наблюдаемое значение критерия достоверности 
по формуле: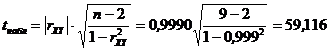 
;
– найдем стандартное значение критерия достоверности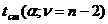 
по таблицам значений коэффициентов Стьюдента (Приложение 4): 
;
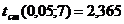– сравнение с 
показывает, что >.
Вывод 2: При уровне значимости 
можно утверждать, что и в генеральной совокупности между признаками 
и существует сильная положительная связь.
4) Найдем уравнения регрессии:
на 
вида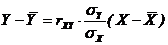 
;
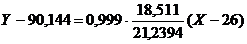
или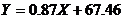 
Построим линию регрессии (рекомендуется строить график на фоне корреляционного поля):
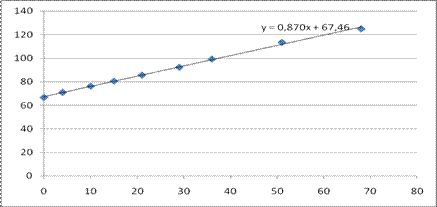
5)
a) Найдем, при какой температуре растворится 100 условных частей 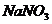. Если 
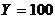получаем, что
;
b) Найдем, сколько условных частей растворится при температуре воды, равной 
. Если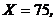 
то получаем, что 
ОДНОФАКТОРНЫЙ ДИСПЕРСИОННЫЙ АНАЛИЗ
Рассмотрим нормально распределенную величину 
, на который действует некоторый нормальный фактор 
, имеющий 
постоянных уровней, причем на всех уровнях распределение значений х является нормальным, а дисперсии одинаковы, хотя и неизвестны.
Пусть число наблюдений при действии каждого из уровней фактора одинаково (
) и результаты представлены в таблице.
Номер испытания | Уровень фактора | ||||
1 |
|
|
| … |
|
2 |
|
|
| … |
|
3 |
|
|
| … |
|
… | … | … | … | … | … |
q |
|
|
| … |
|
Групповая средняя |
|
|
| … |
|
Все значения величины х, наблюдаемые при каждом фиксированном уровне фактора 
, составляют группу, и в последней строке таблицы представлены соответствующие выборочные групповые средние, вычисленные по формуле:
.
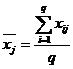В основе однофакторного дисперсионного анализа лежит тесная связь между различием в групповых средних 
и соотношением между двумя видами дисперсий – остаточной и факторной, которые рассчитываются по формулам:
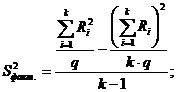
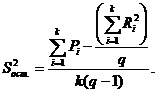
Здесь 
- сумма значений величины 
на уровне ;
- сумма квадратов значений величины на уровне .
В математической статистике доказывается, что факторная дисперсия характеризует влияние фактора на величину , а остаточная – влияние случайных причин. Поэтому, если окажется, что 
, следует сделать вывод об отсутствии существенного влияние фактора на . Если же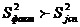 
, необходимо проверить значимость различия этих дисперсий, т. е. при заданном уровне значимости 
проверить нулевую гипотезу о равенстве соответствующих генеральных дисперсий (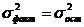
) при конкурирующей гипотезе(
). Если проверка покажет значимость различия между 
(число степеней свободы которой 
) и (число степеней 
, следует сделать вывод о значимости различия между групповыми средними, т. е. о существенном влиянии фактора на . Если различие незначимо, такого вывода сделать нельзя.
|
Из за большого объема этот материал размещен на нескольких страницах:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 |
Основные порталы (построено редакторами)