Задачи 21–30
21)Завод выпускает для магнитофонов три типа предохранителей. Доля каждого из них в общем объеме продукции составляет 30% , 50% , 20%, соответственно. При перегрузке сети предохранитель первого типа срабатывает с вероятностью 0,8, второго – 0,9 и третьего– 0,85. Определить вероятность того, что: а) выбранный наудачу предохранитель не сработает при перегрузке сети; б) предохранитель, который не сработал при перегрузке сети, принадлежит к первому типу?
22)В продукции кондитерской фабрики шоколадные конфеты составляют 40% ассортимента. В среднем 10 из 1000 шоколадных конфет оказываются с браком. Для остальной продукции этот показатель равен 5 из 200, Найти вероятность того, что; а) выбранное наугад изделие окажется без брака; б) выбранное наугад изделие без брака оказалось шоколадной конфетой.
23)Турист может пообедать в трех столовых города. Вероятность того, что он отправится к первой столовой - 1/5 , ко второй - 3/5 и к третьей - 1/5. Вероятности того, что эти столовые закрыты следующие: первая - 1/6, вторая - 1/5 и третья - 1/8. Определить вероятность того, что: а) турист пообедал в одной из выбранных столовых; б) столовая, в которой пообедал студент, оказалась второй столовой?
24)На фабрике, изготавливающей некоторую продукцию, первая машина производит 30% , вторая - 45% , третья - 25% всех изделий. Брак их продукции составляет соответственно 2%, 5% и 3%. Найти вероятность того, что: а) случайно выбранное изделие оказалось дефектным; 6) случайно выбранное изделие произведено первой машиной, если оно оказалось дефектным.
25) Один из трех стрелков вызывается на линию огня и производит выстрел. Вероятность попадания в мишень при одном выстреле для первого стрелка равна 0,3, для второго - 0.5, для третьего – 0,8. Найти вероятность того, что: а) мишень будет поражена одним из, стрелков; б) мишень была поражена выстрелом, произведенным 2-м стрелком.
26)В часовую мастерскую поступают в среднем 40% часов с дефектом А, 25% с дефектом В и 35% с дефектом С. Вероятность ремонта часов с дефектом А равна 0,6, с дефектом B - 0,7, с дефектом С - 0,8. Найти вероятность того, что: а) часы, поступившие в ремонт, будут полностью отремонтированы; б) полностью отремонтированные часы имели дефект А.
27)На склад поступает продукция трех фабрик, причем продукция первой фабрики составляет 20 %, второй - 46%, третьей - 34%. Известно, что средний процент нестандартных изделий для первой фабрики равен 3%, для второй - 2% , для третьей - 1 %. Найти вероятность того, что: а) наудачу взятое изделие окажется нестандартным; б) наудачу взятое изделие произведено на первой фабрике, если оно изделие оказалось нестандартным.
28)В специализированную больницу поступают в среднем 50% больных с заболеванием К, 30% с заболеванием N, 29% с заболеванием М. Вероятность полного излечения от болезни К равна 0,7, для болезней N и М эта вероятность соответственно равна 0,8 и 0,9. Определить: а) вероятность выздоровления больного; б) вероятность того, что выздоровевший больной страдал заболеванием К.
29)Предположим, что 5% всех мужчин и 0,25% всех женщин страдает дальтонизмом. Найти вероятность того, что наугад выбранное лицо страдает дальтонизмом. Какова вероятность того, что это мужчина?
30)Имеются 2 урны: в первой 3 белых и 2 черных, а во второй 4 белых и 4 черных шаров. Из первой урны во вторую перекладывают, не глядя, два шара. После этого их 2-й урны берут один шар. Найти: 1) вероятность того, что этот шар будет белым; 2) вероятность того, что из первой урны наугад переложили 2 белых шара, если из второй урны был вынут белый шар.
Задание 4. Основные теоремы повторных независимых случайных событий, простейший поток событий)
Задачи 31–40
31)В машбюро 5 пишущих машинок. Вероятность того, что каждая из них в течение года потребует ремонта, равна 0,2. Найти вероятность того, что в течение года не придется ремонтировать хотя бы две машинки.
32)В магазин вошли 5 покупателей. Найти вероятность того, что не менее трех из них совершат покупки, если вероятность совершить покупку для каждого вошедшего одна и та же и равна 0,3.
33)Рабочий обслуживает 5 одинаковых станков. Вероятность того, что в течение часа станок потребует регулировки, равна 1/3. Какова вероятность того, что в течение часа рабочему придется регулировать 4 станка?
34)В партии товаров имеется 400 изделий, Вероятность того, что изделие будет высшего сорта, равна 0,8. Какова вероятность того, что а) в партии товаров окажется ровно 320 изделий высшего сорта; б) число изделий высшего сорта в партии товаров будет от 310 до 330?
35) В результате проверки качества приготовленного посева зерна установлено, что 90% зёрен всхожи. Для посадки отобрано и высажено 900 зёрен. Найти вероятность того, что: а) из взятых зёрен прорастёт 820 штук; б) прорастёт от 600 до 640 посаженных зёрен.
36)Среди 1100 студентов левши составляют 1%. Чему равна вероятность того, что из общего количества студентов: а) ровно 11 левшей; б) не менее 20 левшей?
37)Среднее число самолетов, прибывших в аэропорт за I минуту, равно 3. Найти вероятность того, что за 2 минуты прибудут: а) не менее 3-х самолетов; б) не более 2; в) 4 самолета.
38)Среднее число кораблей, находящих в порт за 1 час, равно трем. Найти вероятность того, что за 4 часа в порт зайдут: а) 6 кораблей; б) менее 6 кораблей; в) не менее 6 кораблей.
39)Через кассу в магазине в течение 1 минуты проходит в среднем 2 человека. Найти вероятность того, что за 2 минуты пройдет: а) 4 человека; 6) не менее 2-х человек; в) не более 3-х.
40) При работе ЭВМ возникают сбои (нарушения в работе). Среднее число сбоев в сутки равно 2. Найти вероятность того, что: а) за двое суток не произойдет сбоя; б) в течение суток произойдет хотя бы один сбой; в) за трое суток произойдёт не менее 3-х сбоев.
Задание 5. Законы распределения случайных величин
Задачи 41–45
Задан закон распределения дискретной случайной величины 
. Найти:
а) математическое ожидание 
, дисперсию 
и среднеквадратическое отклонение 
;
б) составить функцию распределения случайной величины 
и построить ее график;
в) вычислить вероятности попадания случайной величины в интервал 
, пользуясь составленной функцией распределения ;
г) составить закон распределения случайной величины 
;
д) вычислить математическое ожидание и дисперсию составленной случайной величины 
двумя способами: пользуясь свойствами математического ожидания и дисперсии, а также непосредственно по закону распределения случайной величины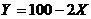
41.
| 10 | 12 | 20 | 25 | 30 |
| 0,1 | 0,2 | 0,1 | 0,2 | 0,4 |
42.
| 10 | 12 | 14 | 16 | 18 |
| 0,2 | 0,3 | 0,1 | 0,2 | 0,2 |
43.
| 4 | 6 | 8 | 10 | 12 |
| 0,2 | 0,3 | 0,1 | 0,2 | 0,2 |
44.
| 30 | 40 | 50 | 60 | 70 |
| 0,2 | 0,2 | 0,2 | 0,3 | 0,1 |
45.
| 2 | 4 | 6 | 8 | 10 |
| 0,2 | 0,3 | 0,1 | 0,2 | 0,2 |
46.
Задачи 46–50
|
Из за большого объема этот материал размещен на нескольких страницах:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 |
Основные порталы (построено редакторами)