Формула Пуассона широко используется в теории массового обслуживания.
Простейший поток событий
Определение. Потоком событий называется последовательность однородных событий, следующих одно за другим в случайные моменты времени (в предельном случае, если события следуют через определенные интервалы).
Вероятность появления ![]() событий простейшего потока за время длительностью
событий простейшего потока за время длительностью 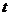 определяется формулой Пуассона:
определяется формулой Пуассона:
![]() , где
, где
![]() – интенсивность простейшего потока, или среднее число событий, появляющихся в единицу времени.
– интенсивность простейшего потока, или среднее число событий, появляющихся в единицу времени.
Примеры решения задач:
Задача 1. Из ящика, где было 4 лопнувших и 12 целых пробирок, вынуто наугад 3 пробирки. Какова вероятность того, что две из них целые?
Решение: Число способов, которыми можно извлечь ![]() пробирки из их общего числа
пробирки из их общего числа ![]() , равно
, равно ![]() – числу сочетаний из
– числу сочетаний из ![]() элементов по
элементов по ![]() и равно числу всех возможных элементарных исходов испытания.
и равно числу всех возможных элементарных исходов испытания.
Найдем число исходов, благоприятствующих интересующему нас событию: среди ![]() пробирок ровно
пробирок ровно ![]() целые.
целые. ![]() целые пробирки можно взять из
целые пробирки можно взять из ![]() целых
целых ![]() различными способами; при этом
различными способами; при этом ![]() пробирок должны быть лопнувшими, взять же
пробирок должны быть лопнувшими, взять же 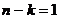 лопнувших пробирок из
лопнувших пробирок из ![]() имеющихся можно
имеющихся можно ![]() различными способами. Следовательно, число благоприятствующих исходов равно
различными способами. Следовательно, число благоприятствующих исходов равно
![]() .
.
Искомая вероятность равна отношению числа исходов, благоприятствующих событию, к числу всех элементарных исходов ![]() :
:
![]() .
.
Вычисления:
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
Ответ: вероятность того, что из 3 наудачу взятых пробирок 2 целые равна 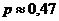 .
.
Задача 2. Центральная городская аптека закреплена за тремя больницами. Вероятность того, что в течение рабочего дня придется отпустить медикаменты первой больнице, равна 0,6, второй больнице – 0,2, третьей – 0,4. Какова вероятность того, что в течение рабочего дня придется отпустить медикаменты: 1) одной больнице? 2) по крайней мере, двум больницам?
Решение: Пусть событие ![]() состоит в том, что аптеке придется отпустить медикаменты первой больнице; вероятность этого события по условию равна
состоит в том, что аптеке придется отпустить медикаменты первой больнице; вероятность этого события по условию равна
![]() ,
,
вероятность противоположного события ![]() – медикаменты отпускаться не будут – будет равна
– медикаменты отпускаться не будут – будет равна
![]() ;
;
событие ![]() состоит в том, что аптеке придется отпустить медикаменты второй больнице; вероятность этого события по условию равна
состоит в том, что аптеке придется отпустить медикаменты второй больнице; вероятность этого события по условию равна
![]() ,
,
вероятность противоположного события ![]() – медикаменты отпускаться не будут – будет равна
– медикаменты отпускаться не будут – будет равна
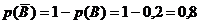 ;
;
событие ![]() состоит в том, что аптеке придется отпустить медикаменты третьей больнице; вероятность этого события по условию равна
состоит в том, что аптеке придется отпустить медикаменты третьей больнице; вероятность этого события по условию равна
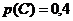 ,
,
вероятность противоположного события ![]() – медикаменты отпускаться не будут – будет равна
– медикаменты отпускаться не будут – будет равна
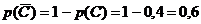 .
.
1) Событие ![]() – аптеке придется отпустить медикаменты одной аптеке – реализуется следующим образом:
– аптеке придется отпустить медикаменты одной аптеке – реализуется следующим образом:
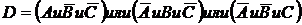 .
.
Для нахождения вероятности этого события используем теоремы умножения и сложения вероятностей событий: ![]()
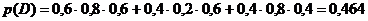
2) Событие ![]() – аптеке придется отпустить лекарство, по крайней мере, двум (т. е. двум или трем) больницам – включает в себя следующие события:
– аптеке придется отпустить лекарство, по крайней мере, двум (т. е. двум или трем) больницам – включает в себя следующие события:
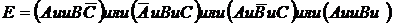 .
.
Для нахождения вероятности этого события используем теоремы умножения и сложения вероятностей событий:
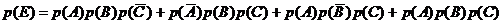 , или
, или
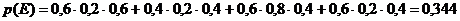 .
.
Ответ: 1) вероятность того, что центральной городской аптеке в течение рабочего дня придется отпустить медикаменты одной больнице, равна ![]() ; 2) вероятность того, что центральной городской аптеке в течение рабочего дня придется отпустить медикаменты, по крайней мере, двум больницам, равна
; 2) вероятность того, что центральной городской аптеке в течение рабочего дня придется отпустить медикаменты, по крайней мере, двум больницам, равна ![]() .
.
Задача 3. В цехе установлено 5 датчиков предельно допустимой концентрации пыли в воздухе, каждый из которых может включать систему сигнализации. Вероятность срабатывания первого датчика равна 0,8, второго – 0,9, третьего – 0,85, четвертого – 0,7, пятого – 0,75. 1) Найти вероятность того, что по достижении предельно допустимой концентрации пыли сигнализация сработает? 2) Сигнализация сработала. Какова вероятность того, что сигнализацию включил третий датчик?
Решение: Пусть событие ![]() состоит в том, что сигнализация сработала. Это событие может произойти только в случае появления одного из несовместных событий
состоит в том, что сигнализация сработала. Это событие может произойти только в случае появления одного из несовместных событий ![]() – включение
– включение ![]() датчиком сигнализации. Вероятности событий
датчиком сигнализации. Вероятности событий 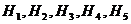 по условию одинаковы и равны
по условию одинаковы и равны ![]() . События
. События ![]() образуют полную группу, т. к.
образуют полную группу, т. к.![]() .
.
Известны условные вероятности события ![]()
![]() – вероятности срабатывания
– вероятности срабатывания ![]() датчика:
датчика:
![]()
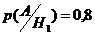 ,
, ![]() ,
, ![]() ,
, ![]() ,
,![]() .
.
1) Вероятность события ![]() вычислим по формуле полной вероятности:
вычислим по формуле полной вероятности:
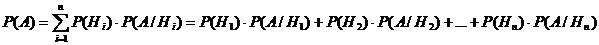 , или
, или 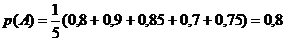 .
.

|
Из за большого объема этот материал размещен на нескольких страницах:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 |
 Основные порталы (построено редакторами)
Основные порталы (построено редакторами)

