б) 
, т. е. 
. Согласно теореме сложения вероятностей получаем, что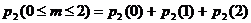 
. Воспользуемся вычислениями, сделанными в предыдущем пункте, и получим, что 
;
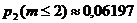в) 
. В данном случае искомая вероятность
вычисляется по формуле Пуассона: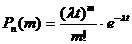 
и будет равна 
.
Ответ: вероятность того, что за 2 минуты прибудут: а) не менее 3-х самолетов, равна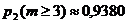 
; б) не более 2, равна 
; в) 4 самолета, равна 
.
ОСНОВЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ. СЛУЧАЙНЫЕ ВЕЛИЧИНЫ
Определение. Величина, принимающая свои значения в зависимости от исходов некоторого испытания, причем для каждого элементарного исхода имеющая одно единственное значение, называется случайной.
Дискретная случайная величина
Определение. Величина, принимающая отдельные, изолированные возможные значения с определенными вероятностями называется дискретной случайной величиной.
Числовые характеристики дискретной случайной величины
Математическое ожидание
Определение. Математическим ожиданием 
дискретной случайной величины 
называется сумма произведений всех возможных ее значений на соответствующие им вероятности: 
Свойства математического ожидания
1. Математическое ожидание постоянной величины равно самой постоянной: 
, где 
.
2. Математическое ожидание алгебраической суммы нескольких случайных величин равно алгебраической сумме математических ожиданий этих величин: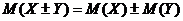 
.
Следствие. Если 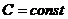, то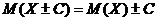 
.
3. Математическое ожидание произведения нескольких взаимно независимых случайных величин равно произведению математических ожиданий этих величин: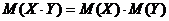 
.
Следствие. Постоянный множитель можно выносить за знак математического ожидания: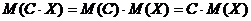 
, где .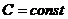
4. Математическое ожидание числа появлений события 
в 
независимых испытаниях (математическое ожидание биноминального распределения) равно произведению числа испытаний на вероятность появления события в каждом испытании: 
.
Дисперсия
Определение. Дисперсией 
дискретной случайной величины называется математическое ожидание квадрата отклонения этой величины от ее математического ожидания:
.
Для вычисления дисперсии также можно использовать следующую формулу:
,
т. е. дисперсия случайной величины равна разности между математическим ожиданием квадрата этой величины и квадратом её математического ожидания.
Свойства дисперсии
1. Дисперсия постоянной величины равна нулю: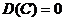 
,
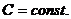
2. Постоянный множитель можно выносить за знак дисперсии, предварительно возведя его в квадрат: 
,
3. Дисперсия суммы нескольких взаимно независимых случайных величин равна сумме дисперсий этих величин: 
4. Дисперсия разности двух независимых случайных величин равна сумме дисперсий этих величин: 
5. Если , то 
Замечание 2. Для вычисления дисперсии биноминального распределения можно воспользоваться следующей формулой: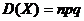 
, где – число испытаний; 
– вероятность осуществления события в одном испытании; 
– вероятность осуществления события 
(противоположного событию ) в одном испытании.
Среднеквадратическое отклонение
Определение. Среднеквадратическим отклонением случайной величины называется квадратный корень из дисперсии:
Замечание 3. На основании данного определения для обозначения дисперсии часто используется символ 
.
Интегральная функция распределения
Для количественной характеристики распределения случайной величины вводится понятие интегральной функции pacпределения 
случайной величины.
Определение. Интегральной функцией распределения называют функцию , определяющую для каждого значения вероятность того, что случайная величина примет значение меньше 
, т. е.
.
Свойства функции распределения
1. Значения интегральной функции распределения принадлежат отрезку 
.
2. Функция распределения есть неубывающая функция, т. е. если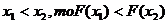 
.
Следствие 1. Вероятность того, что случайная величина попадёт в интервал 
, равна приращению её интегральной функции распределения на интервале : 
.
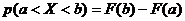Следствие 2. Вероятность того, что непрерывная случайная величина примет одно определённое, заранее заданное значение равна нулю: 
.
3. Если возможные значения случайной величины принадлежат интервалу , то 
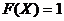при 
, 
при 
.
|
Из за большого объема этот материал размещен на нескольких страницах:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 |
Основные порталы (построено редакторами)