Коэффициент парной корреляции измеряет степень и определяет направление только прямолинейных связей. Коэффициент парной корреляции rxy есть безразмерная величина, значения которой принадлежат отрезку: ![]() .
.
При отрицательной корреляционной связи увеличение одной из переменных ведет к уменьшению другой. Соответствие между значениями rxy и характером связи может быть представлено следующей таблицей (шкала Чеддока):
Значение коэффициента парной корреляции, | Связь |
1 | Функциональная |
>0,9 | Очень сильная |
0,7 – 0,9 | Сильная (тесная) |
0,5 – 0,7 | Значительная (заметная) |
0,3 – 0,5 | Умеренная |
<0,3 | Слабая |
0 | Отсутствует |
Выборочный коэффициент парной корреляции rxy вычисляется по формуле: 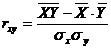 ,
,
здесь 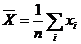 - выборочная средняя признака
- выборочная средняя признака ![]() ;
;
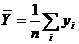 - выборочная средняя признака
- выборочная средняя признака ![]() ;
;
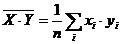
![]() - среднее значение произведений
- среднее значение произведений ![]() и
и ![]() ;
;
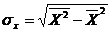 - среднеквадратическое отклонение признака
- среднеквадратическое отклонение признака ![]() ;
;
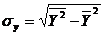 - среднеквадратическое отклонение признака
- среднеквадратическое отклонение признака ![]() ;
;
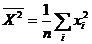 - среднее значение квадрата признака
- среднее значение квадрата признака ![]() ;
;
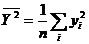 - среднее значение квадрата признака
- среднее значение квадрата признака ![]() ;
;
![]() - квадрат среднего значения признака
- квадрат среднего значения признака ![]() ;
;
![]() - квадрат среднего значения признака
- квадрат среднего значения признака ![]() .
.
Достоверность значения выборочного коэффициента парной корреляции rxy проверяется следующим образом:
- вычисляют наблюдаемое значение критерия достоверности tнабл. по формуле: 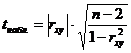 , здесь
, здесь ![]() – объём выборки;
– объём выборки;
- находят стандартное значение критерия достоверности 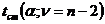 по таблицам значений коэффициентов Стьюдента (Приложение 4).;
по таблицам значений коэффициентов Стьюдента (Приложение 4).;
- сравнивают tнабл. с tст ![]() .
.
Если tнабл. > tсm, то при уровне значимости ![]() делают вывод о достоверности найденного значения rxy. В этом случае с (доверительной) вероятностью
делают вывод о достоверности найденного значения rxy. В этом случае с (доверительной) вероятностью ![]() (или р) можно считать, что между коррелирующими признаками имеется связь и в генеральной совокупности такая же по характеру, какая получилась в выборке.
(или р) можно считать, что между коррелирующими признаками имеется связь и в генеральной совокупности такая же по характеру, какая получилась в выборке.
Если tнабл.![]() tcm, то выборочный коэффициент корреляции недостоверен при уровне значимости
tcm, то выборочный коэффициент корреляции недостоверен при уровне значимости ![]() , а, значит, у нас нет возможности сделать какое-либо заключение о связи признаков в генеральной совокупности. Для выяснения этого вопроса требуется провести повторные испытания на более многочисленном материале, т. е. увеличить объем выборки.
, а, значит, у нас нет возможности сделать какое-либо заключение о связи признаков в генеральной совокупности. Для выяснения этого вопроса требуется провести повторные испытания на более многочисленном материале, т. е. увеличить объем выборки.
Помимо наличия связи, статистика позволяет найти уравнения, описывающие зависимость между признаками. Такая зависимость называется функцией регрессии или регрессией. При линейных связях функция регрессии имеет вид: 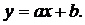 Параметры
Параметры ![]()
![]() уравнения определяются методом наименьших квадратов.
уравнения определяются методом наименьших квадратов.
Уравнение регрессии:
![]() на
на ![]() :
: 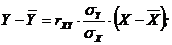
Уравнение регрессии позволяет прогнозировать возможные значения зависимых переменных, иначе, позволяет предсказывать поведение одного из параметров при целенаправленном изменении другого.
Пример решения задач:
Пример. В книге "Основы химии" Д. И. Менделеева приводятся данные о растворимости азотнокислого натрия в зависимости от температуры воды. В 100 частях воды растворяется следующее число условных частей 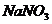 (
(![]() ) при соответствующих температурах (
) при соответствующих температурах (![]() ) раствора:
) раствора:
| 0 | 4 | 10 | 15 | 21 | 29 | 36 | 51 | 68 |
| 66,7 | 71,0 | 76,3 | 80,6 | 85,7 | 92,9 | 99,4 | 113,6 | 125,1 |
Требуется:
1) построить корреляционное поле;
2) предполагая, что данная зависимость между ![]() и
и ![]() близка к линейной, найти выборочный коэффициент корреляции
близка к линейной, найти выборочный коэффициент корреляции ![]() ;
;
3) проверить достоверность найденного значения выборочного коэффициента корреляции при уровне значимости ![]() ;
;
4) найти уравнение регрессии ![]() на
на ![]() и построить линию регрессии на фоне корреляционного поля;
и построить линию регрессии на фоне корреляционного поля;
5) используя уравнение регрессии, найти, при какой температуре раствориться 100 условных частей ![]() и сколько условных частей
и сколько условных частей ![]() растворится при
растворится при ![]() .
.
Решение:
1) Построим корреляционное поле. Для этого на координатную плоскость нанесем точки ![]()
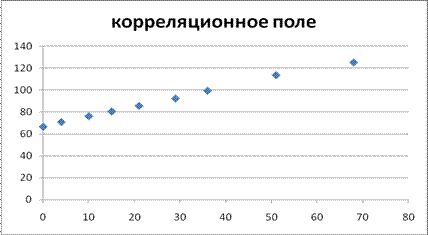
2)Для вычисления выборочного коэффициента парной корреляции ![]() используем формулу:
используем формулу: ![]() .
.
Промежуточные вычисления выполним в таблице:
№ |
|
|
|
|
|
1 | 0 | 66,7 | 0 | 0 | 4448,89 |
2 | 4 | 71,0 | 284 | 16 | 5041 |
3 | 10 | 76,3 | 763 | 100 | 5821,69 |
4 | 15 | 80,6 | 1209 | 225 | 6496,36 |
5 | 21 | 85,7 | 1799,7 | 441 | 7344,49 |
6 | 29 | 92,9 | 2694,1 | 841 | 8630,41 |
7 | 36 | 99,4 | 3578,4 | 1296 | 9880,36 |
8 | 51 | 113,6 | 5793,6 | 2601 | 12904,96 |
9 | 68 | 125,1 | 8506,8 | 4624 | 15650,01 |
| 234 | 811,3 | 24628,6 | 10144 | 76218,17 |
Вычисляем: ![]() ;
; 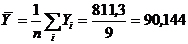 ;
;

|
Из за большого объема этот материал размещен на нескольких страницах:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 |
 Основные порталы (построено редакторами)
Основные порталы (построено редакторами)

