Определение. Событие, состоящее в наступлении хотя бы одного из событий 
и 
, (возможно, двух сразу), называется суммой (или объединением) событий и , и обозначается символом 
или 
Событие, противоположное событию , обозначают с помощью символа 
.
Определение суммы и произведения двух событий обобщается на любое число событий.
Понятие вероятности
Классическое определение вероятности
Определение. Вероятностью события называется отношение числа 
равновозможных элементарных исходов, благоприятствующих событию , к общему числу 
всех равновозможных и единственно возможных элементарных исходов.
При классическом определении вероятность события вычисляется по формуле: 
.
Из определения вероятности вытекают следующие свойства:
1. Вероятность любого события есть неотрицательное число, не превышающее 1.
2. Вероятность достоверного события (
) равна 1.
3. Вероятность невозможного события (
) равна 0.
Статистическое определение вероятности
Среди естествоиспытателей весьма широко распространена концепция вероятности, вытекающая из сущности понятия относительной частоты.
Определение. Относительной частотой события называется отношение числа случаев , в которых событие осуществлялось (наблюдалось), к общему числу проведённых испытаний 
.
Относительная частота вычисляется по формуле: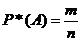 
.
Определение. Вероятностью события в статистическом смысле называется предел относительной частоты события (т. е. отношения частоты события к числу всех проведённых испытаний ) при неограниченном увеличении последних, т. е. 
.
Вычисление вероятностей
Теорема умножения вероятностей
Определение. Вероятность события при условии, что осуществилось событие , называется условной вероятностью события и обозначается следующим образом: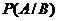 
или 
.
Теорема. Вероятность совместного осуществления двух зависимых событий равна произведению вероятности одного из них на условную вероятность другого при условии, что первое произошло: 
Теорема. Вероятность совместного осуществления двух независимых событий и равна произведению вероятностей этих событий: 
.
Теорема. Вероятность совместного осуществления конечного числа независимых в совокупности событий равна произведению вероятностей этих событий.
Теорема сложения вероятностей несовместных событий
Пусть события и несовместны (
) и заданы вероятности их осуществления: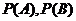 
. Требуется определить вероятность осуществления одного из двух (безразлично какого) этих событий.
Теорема. Вероятность осуществления одного из двух несовместных событий равна сумме вероятностей этих событий: 
.
Следствие. Вероятность осуществления одного из нескольких попарно несовместных событий (безразлично какого) равна сумме вероятностей этих событий: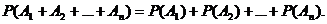 
Следствие. Если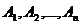 
полная группа событий, то 
Следствие. Если 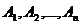полная группа событий, то 
Если событие, противоположное событию , обозначить через , то 
, откуда 
.
Теорема сложения вероятностей совместных событий
Пусть события и совместны и заданы вероятности этих событий и вероятность их совместного появления 
.
Требуется определить вероятность события , состоящего в том, что осуществится хотя бы одно из совместных событий и .
Теорема. Вероятность осуществления хотя бы одного из двух совместных событий равна сумме вероятностей этих событий без вероятности их совместного осуществления: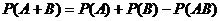 
.
Вероятность осуществления хотя бы одного события
Пусть события независимы в совокупности и вероятности их осуществления известны: 
.
Пусть в результате испытания могут осуществиться все событий, либо часть из них (в частности, только одно или ни одного). Требуется найти вероятность того, что наступит хотя бы одно из этих событий.
Теорема. Вероятность осуществления события , состоящего в наступлении хотя бы одного из событий 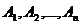, независимых в совокупности, равна разности между единицей и произведением вероятностей противоположных событий 
: 
,
где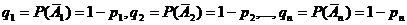 
Формула полной вероятности
Пусть событие может наступить при условии осуществления одного и только одного события 
из полной группы несовместных событий 
. Поскольку заранее неизвестно, какое из этих событий наступит, их называют гипотезами.
|
Из за большого объема этот материал размещен на нескольких страницах:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 |
Основные порталы (построено редакторами)