Геометрическую интерпретацию оптимального решения можно представить следующим образом. Построим прямую, соответствующую случаю, когда целевая функция равна нулю, т. е. 
Если прямую, графически представляющую целевую функцию, передвигать вверх параллельно самой себе, что соответствует увеличению 
, то значение целевой функции уменьшается, и будем минимальным в крайней точке области допустимых значений, в данном случае в вершине В. Координаты этой точке найдем, решив, совместно уравнения 
и 
Получим: 
При этом значение целевой функции 
Если прямую, графически представляющую целевую функцию, передвигать вниз параллельно самой себе, что в данном случае соответствует уменьшению , то значение целевой функции увеличивается, и будет максимальным в вершине С. Координаты этой точки найдем, решив, совместно уравнения и 
Получим: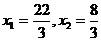 
и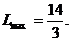 
На практике не всегда в условии задачи дается система ограничений и вид целевой функции, поэтому прежде чем приступить к решению задачи необходимо, согласно условию задачи, составить систему ограничений и вид целевой функции.
Пример решения задач:
Пример. Аптека закупает у населения плоды шиповника по цене 2 руб за 1 кг и рябины по цене 0,5 руб за 1 кг, а затем, расфасовав их, продает по цене соответственно 3 руб и 1 руб за кг. На закупку аптеке разрешено использовать не более 1000 руб., а план закупок составляет 300 кг шиповника и 400 кг рябины. Аптека закупила у населения 400 кг шиповника и 400 кг рябины. Оптимальны ли результаты в отношении прибыли от закупок и продажи плодов? Найти оптимальный план, соответствующий оптимальной прибыли.
Решение: Пусть 
- количество шиповника в кг закупаемое у населения, а 
- рябины в кг. Выражение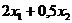 
определяет расходы на закупку шиповника и рябины, по условию они не должны превышать 1000 руб, следовательно 
Причем по плану закупок 
, а 
. Прибыль аптеки составит в рублях 
Целью аптеки, по условию задачи, является получение максимальной прибыл, т. е.
.
Таким образом, система ограничений имеет вид:
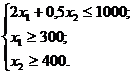
а целевая функция 
Геометрически система ограничений выглядит следующим образом:
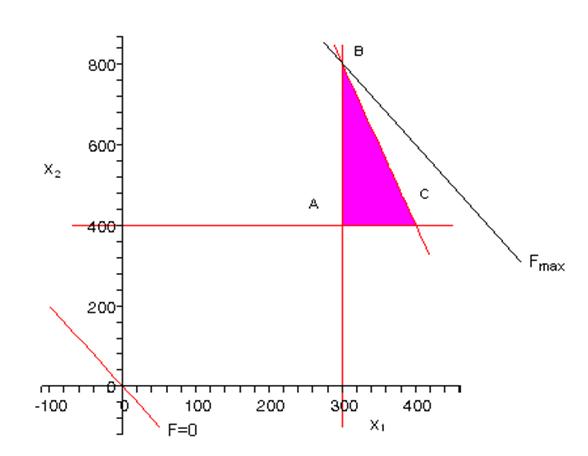
Если прямую, графически представляющую целевую функцию 
, передвигать в направлении области допустимых решений (заштрихована) параллельно самой себе, то значение целевой функции увеличивается, и будет максимальным в крайней точке области допустимых значений, в данном случае в вершине В. Координаты этой точки найдем, решив, совместно уравнения 
и 
Получим: 
. При этом значение целевой функции 
Найдем значение целевой функции при 
: 
Сравнивая с 
, делаем вывод: осуществленный аптекой план закупок не является оптимальным.
Ответ: ,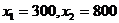
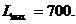
КОНТРОЛЬНЫЕ ЗАДАНИЯ
Задание 1. Понятие вероятности случайных событий
Задачи 1–10
1) Из полной колоды карт (52 карты) вынимаются наугад сразу 3 карты. Найти вероятность того, что этими картами будут тройка, семерка, туз.
2) В ящике лежат 15 красных, 9 синих и 6 зеленых шаров, одинаковых на ощупь. Наудачу вынимают 6 шаров. Какова вероятность того, что вынут 1 зеленый, 2 синих и 3 красных шара.
3) В лотерее выпущено 20 билетов, 10 из которых выигрывают. Куплено 5 билетов. Какова вероятность того, что, по крайней мере, один из купленных билетов выигрышный?
4) Владелец одной карточки лотереи "Спортлото'' (6 из 49) зачеркивает 6 номеров. Какова вероятность того, что им будет угадано 5 номеров в очередном тираже?
5) Из партии, в которой 30 деталей без дефекта и 5 с дефектом, берут наудачу 3 детали. Найти вероятность того, что, по крайней мере, одна деталь без дефекта.
6) В партии из 10 деталей имеются 4 бракованных. Какова вероятность того, что среди наудачу отобранных 5 деталей окажутся 2 бракованные.
7) В урне 10 шаров, из которых 2 белых, 3 черных и 5 синих. Наудачу вынули 3 шара. Какова вероятность того, что все 3 шара разного цвета?
8) В бригаде, состоящей из 4 женщин и 3 мужчин, разыгрываются 4 билета в театр. Какова вероятность того, что среди обладателей билетов окажется 2 женщины и 2 мужчин?
9) В группе из 25 студентов, среди которых 10 девушек, разыгрываются 5 билетов. Определить вероятность того, что среди обладателей билетов окажутся две девушки.
10)В урне б белых, 4 черных и 5 красных шаров. Из урны наугад вынимают 5 шаров. Найти вероятность тоге, что среди них окажутся 2 белых и 1 черный шар.
Задание 2. Основные теоремы случайных событий (теоремы сложения и умножения)
Задачи 11–20
11)Вероятность попадания в мишень для первого стрелка - 0,8, а для второго - 0,6. Стрелки независимо друг от друга сделали по одному выстрелу. Какова вероятность того, что в мишень попадет только один из стрелков? По крайней мере, один стрелок?
12)Охотник выстрелил три раза по удаляющейся цели. Вероятность попадания в нее в начале стрельбы равна 0,8, а после каждого выстрела уменьшается на 0,1. Найдите вероятность того, что он: а) промахнется вес 3 раза; б) попадет хотя бы один раз; в) попадет 2 раза.
13)Вероятность поражения первой мишени для данного стрелка 9/13.Если при первом выстреле зафиксировано попадание, то стрелок получает право на второй выстрел по другой мишени. Вероятность поражения обеих мишеней при двух выстрелах 0,5. Определить вероятность поражения второй мишени.
14)Четыре охотника договорились стрелять по дичи в определенной последовательности. Следующий охотник производит выстрел лишь в случае промаха предыдущего. Вероятность попадания в цель каждым из охотников одинакова и равна 0,8. Найти вероятность того, что будет произведено: а) один; б) два; в) три; г) четыре выстрела.
15)Для сообщения об аварии установлены два независимо работающих сигнализатора-автомата. Вероятность того, что при аварии сработает первый автомат, равна 0,95; второй - 0,9. Найти вероятность того, что при аварии поступит сигнал: а) хотя бы от одного сигнализатора; б) только от одного сигнализатора.
16)Экзаменационный билет содержит 3 вопроса. Вероятности того, что студент ответит на первый и второй вопросы билета, равны 0,9; на третий - 0,8. Найти вероятность того, что студент сдаст экзамен, если для этого необходимо ответить хотя бы на два вопроса.
17)Рабочий обслуживает три станка. Вероятность того, что в течение смены потребует его внимания первый станок, равна 0,7, второй - 0,75, третий - 0,8. Найти вероятность того, что в течение смены внимания рабочего а) потребуют какие-либо два станка; б) хотя бы один станок.
18)Два стрелка производят в цель по одному выстрелу. Вероятность попадания для первого стрелка равна 0,7, для второго - 0,8. Найти вероятность того, что попадут в цель: а) оба; б) только один; в) ни один; г) хотя бы один.
19)Рабочий обслуживает четыре станка. Вероятность того, что в течение часа первый станок не потребует внимания рабочего, равна 0,3, второй - 0,4, третий - 0,7, четвертый - 0,4. Найти вероятность того, что в течение часа а) ни один станок не потребует внимания рабочего; б) хотя бы один станок потребует внимания рабочего.
20)Радист трижды вызывает корреспондента. Вероятность того, что будет принят первый вызов, равна 0,2, второй - 0,3, третий - 0,4. Найти вероятность того, что корреспондент услышит вызов радиста.
Задание 3. Основные теоремы случайных событий (полная вероятность и формула Байеса)
|
Из за большого объема этот материал размещен на нескольких страницах:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 |
Основные порталы (построено редакторами)