3) математическое ожидание случайной величины
; дисперсию случайной величины (двумя способами) и среднеквадратическое отклонение; постройте графики интегральной 
и дифференциальной 
функций;
4) вероятность попадания величины в интервал (
) двумя способами (используя интегральную и дифференциальную функции), а затем проиллюстрируйте этот результат на графиках и .
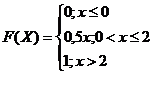
Решение:
1) Если функция является функцией распределения и если возможные значения случайной величины принадлежат интервалу 
, то 
, если 
, 
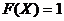, если 
. Проверим это. По условию 
, тогда 
. Таким образом, заданная функция является функцией распределения.
2) Дифференциальной функцией распределения 
называется производная от интегральной функции: 
.
Следовательно, получаем:
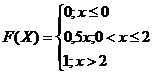
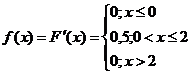
3) Для вычисления числовых характеристик случайной величины воспользуемся формулами:
– 
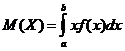, где – плотность вероятности случайной величины 
и если возможные значения случайной величины принадлежат отрезку 
;
–
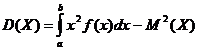, если возможные значения случайной величины принадлежат отрезку ;
–
.
Вычисляем:
;
;
.
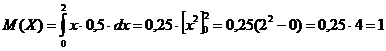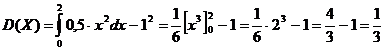График интегральной функции непрерывной случайной величины X рис 2.
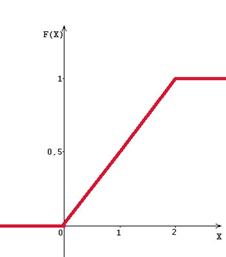
Рис 2. График интегральной функции непрерывной случайной величины X
График дифференциальной функции непрерывной случайной величины X рис 3.
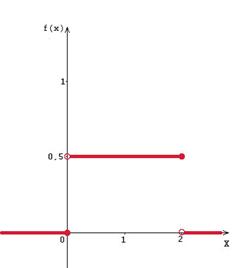
Рис 3. График дифференциальной функции непрерывной случайной величины X
4) Вычислим вероятность попадания величины в интервал (), используя интегральную функцию : вероятности попадания случайной величины в интервал 
вычислим по формуле 
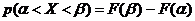. В данном случае 
, следовательно 
. Вычислим вероятность попадания величины в интервал (), используя дифференциальную функцию : 
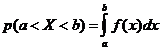. В данном случае 
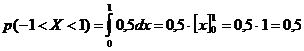, т. к. 
, если 
.
Задача 3. Случайная величина распределена нормально с математическим ожиданием 
. Вероятность попадания в интервал 
равна 0,2. Чему равна вероятность попадания в интервал (35;40)?
Решение
1) По известной вероятности попадания в заданный интервал найдем среднеквадратическое отклонение 
. Для этого воспользуемся формулой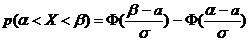 
. Согласно условию , 
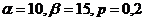, т. е.
или 
,
или
,
или 
.
По таблице значений функции 
находим (Приложение 2), что 
, если 
,
следовательно, 
.
2) Вероятность попадания в интервал (35;40) найдем, используя ту же формулу, тогда
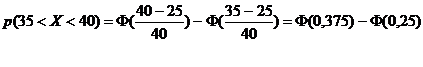
По таблице значений функции 
находим, что 
, а вероятность 
.
ЭЛЕМЕНТЫ МАТЕМАТИЧЕСКОЙ СТАТИСТИКИ
Статистический анализ результатов исследований
Статистика – это наука, изучающая методы обработки результатов наблюдений массовых случайных явлений, обладающих закономерностью, с целью выявления этой закономерности.
При решении многих практических задач, связанных со статистическими моделями, необходимые вероятностные характеристики случайных величин неизвестны и должны определяться по экспериментальным данным.
Такое статистическое описание результатов экспериментов, построение и проверка различных математических моделей, использующих понятие вероятности, составляют основное содержание математической статистики.
Методы математической статистики расширяют возможности научного предсказания и целесообразного принятия решений в условиях неопределенности, когда принципиально не может быть известен полный комплекс условий проведения эксперимента.
Основополагающими понятиями статистической теории являются понятия генеральной совокупности и выборки.
Определение. Совокупность, состоящая из всех объектов, которые могут быть к ней отнесены, называется генеральной.
|
Из за большого объема этот материал размещен на нескольких страницах:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 |
Основные порталы (построено редакторами)