Теория вероятностей и математическая статистика (стр. 20 )

Случайная величина задана интегральной функцией распределения . Требуется убедиться, что заданная функция является функцией распределения некоторой случайной величины, проверив свойства . В случае положительного ответа найдите: а) дифференциальную функцию ; в) математическое ожидание случайной величины; c) дисперсию случайной величины (двумя способами) и среднеквадратическое отклонение; d) построить графики интегральной и дифференциальной f(x) функций; e) определить вероятность попадания величины в интервал ( ) двумя способами (используя интегральную и дифференциальную функции), а затем проиллюстрировать этот результат на графиках и .

46.

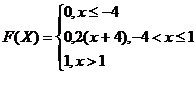
47.

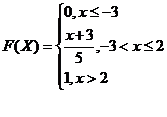
48.

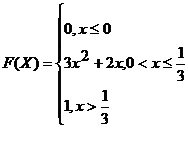
49.

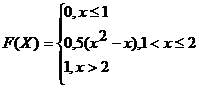
50.

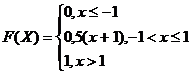
Задание 6. Нормальный закон распределения

Найти вероятность попадания в заданный интервал нормально распределенной случайной величины, если известны ее математическое ожидание и среднеквадратическое отклонение .

51) , , ,

52) , , ,

53) , , ,

54) , , ,

55) , , ,

56) , , ,

57) , , ,

58) , , ,

59) , , ,

60) , , ,

Задание 7. Первичный анализ выборочных данных (рекомендуется использовать Excel);

Из таблицы значений некоторого признака сделайте выборку согласно номеру задачи своего варианта и выполните статистическую обработку данных по следующей схеме:

1) выполнить ранжирование признака и составить безинтервальный вариационный ряд распределения, выбрав его значений (согласно своему варианту);

2) составить равноинтервальный вариационный ряд, разбив всю вариацию на интервалов;

3) построить гистограмму распределения;

4) найти числовые характеристики выборочной совокупности:

– характеристики положения (выборочную среднюю, моду, медиану);

– характеристики рассеяния (выборочную дисперсию, среднеквадратическое отклонение, коэффициент вариации, показатели асимметрии и эксцесса)

5) по результатам обработки выборочных данных (на основании выполнения свойств нормального распределения и вида гистограммы) выдвинуть гипотезу о нормальном распределении генеральной совокупности и проверить ее:

– используя правило «»;

– с помощью коэффициентов асимметрии и эксцесса на уровне значимости ;

6) построить полигон распределения и кривую нормального распределения по опытным данным, приняв в формуле Гаусса математическое ожидание и ;

7) найти доверительный интервал для генеральной средней . Принять уровень значимости .

61. Номера значений с 1 по 40

62. Номера значений с 21 по 60

63. Номера значений с 41 по 80

64. Номера значений с 61 по 100

65. Номера значений с 81 по 120

66. Номера значений с 101 по 140

67. Номера значений с 121по 160

68. Номера значений с 141по 180

69. Номера значений с 161по 200

70. Номера значений с 1 по 20 и с 181по 200

Таблица значений признака

№	Значения признака, полученные в результате эксперимента
1–10	84	91	87	83	90	69	100	96	79	94
11–20	93	86	81	83	84	92	93	85	84	88
21–30	63	87	87	81	95	90	69	95	96	84
31–40	82	79	88	90	92	80	81	85	81	83
41–50	84	96	86	94	85	92	79	75	94	66
51–60	88	79	89	75	92	79	78	95	84	91
61–70	91	74	73	73	85	85	76	83	76	86
71–80	71	85	92	84	90	82	90	73	89	87
81–90	72	96	85	95	91	76	94	95	84	96
91–100	77	85	103	96	97	84	78	93	92	89
101–110	83	86	96	89	87	83	79	79	95	90
111–120	77	91	87	88	89	78	86	85	78	79
121–130	82	68	71	87	89	89	81	81	70	79
131–140	88	104	91	97	77	88	86	79	86	72
141–150	77	85	93	85	87	83	76	79	90	91
151–160	84	74	76	75	93	103	80	96	100	95
161–170	102	81	75	80	90	85	82	77	94	102
171–180	87	95	99	83	80	93	90	79	93	106
181–190	95	85	84	90	93	95	98	88	79	91
191–200	86	88	93	80	103	88	90	68	89	90