Пусть известны вероятности 
этих гипотез и условные вероятности 
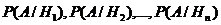
события А. Требуется найти вероятность события 
.
Теорема. Вероятность события , которое может наступить лишь при условии осуществления одного из несовместных событий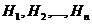 
, образующих полную группу событий 
, равна сумме произведений вероятностей каждой из этих гипотез на соответствующую условную вероятность события : 
.
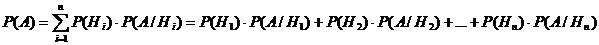Данную формулу называют формулой полной вероятности.
Формула Бейеса
Пусть событие может наступить при условии осуществления одного из несовместных событий (гипотез 
) , образующих полную группу событий. Пусть вероятности известны до опыта. Производится опыт, в результате которого осуществляется событие . Требуется переоценить вероятности гипотез при условии, что событие уже произошло. Переоценка вероятностей гипотез может быть осуществлена по формуле проверки гипотез (формуле Бейеса):
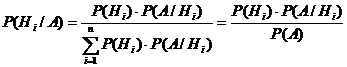
Таким образом, вероятность гипотезы после опыта равна дроби, числителем которой является произведение вероятности этой гипотезы до опыта на вероятность события по этой гипотезе, а знаменателем – сумма таких же произведений для всех возможных в данном случае гипотез (или полная вероятность события ).
Повторные независимые испытания. Формула Бернулли
Пусть производится 
независимых повторных испытаний, в каждом из которых событие имеет одну и ту же вероятность 
, не зависящую от номера испытания (вероятность события 
, противоположного событию , также постоянна и равна 
).
Требуется найти вероятность 
того, что в 
испытаниях событие произойдёт ровно 
раз.
Данная задача решается с помощью формулы Бернулли:
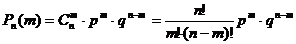
Эту формулу называют также формулой биномиального распределения, так как её правая часть представляет собой общий член разложения бинома Ньютона.
При большом числе испытаний вычисление по формуле Бернулли сопряжено с громоздкостью вычислений. Чтобы избежать этих затруднений, целесообразно использовать формулы, позволяющие приближённо определять вероятности , 
,
,
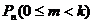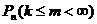, с которыми происходит событие .
Локальная теорема Лапласа
Теорема. Вероятность того, что в независимых испытаниях, в каждом из которых вероятность осуществления события постоянна и равна p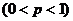
, событие наступит ровно раз, приближённо равна (тем точнее, чем больше ):
, где 
, 
.
Таблица для положительных значений функции Гаусса 
приведена в Приложение 1 данного пособия. Поскольку функция – чётная, т. е. 
, то для отрицательных значений аргумента пользуются этой же таблицей.
Интегральная теорема Лапласа
Довольно часто требуется найти вероятность того, что в условиях схемы Бернулли событие , имеющее постоянную вероятность, при испытаниях появляется не менее 
раз и не более 
раз.
Данная вероятность может быть найдена с помощью интегральной теоремы Лапласа.
Теорема. Вероятность того, что в независимых испытаниях, в каждом из которых вероятность осуществления события постоянна и равна 
, событие наступит не менее раз и не более раз приближённо равна:
,
здесь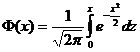 
– стандартный интеграл вероятностей (функция Лапласа),
, 
.
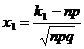Таблица для неотрицательных значений функции Лапласа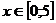
приведена в Приложении 5 данного пособия. Полагают, что для значений 
.
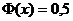Если 
, то используют таблицу Приложение 2 с учётом того, что функция Лапласа есть функция нечётная, т. е. 
.
Закон Пуассона – закон редких событий
Пусть требуется найти вероятность того, что при очень большом числе испытаний, в каждом из которых вероятность осуществления события очень мала, событие наступит ровно раз.
В этом случае ни формула Бернулли, ни асимптотическая формула Лапласа не могут быть практически использованы для решения поставленной задачи.
При больших , малых 
и если выполняется условие 
, то для вычисления искомой вероятности применяют формулу Пуассона (закон Пуассона):
, где 
.
|
Из за большого объема этот материал размещен на нескольких страницах:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 |
Основные порталы (построено редакторами)