Следствие 3. Если возможные значения случайной величины ![]() расположены на всей числовой оси, то справедливы следующие предельные соотношения:
расположены на всей числовой оси, то справедливы следующие предельные соотношения: ![]() ,
, ![]() .
.
Для дискретной случайной величины функция распределения определяется по формуле: ![]() , где неравенство
, где неравенство ![]() под знаком суммы указывает, что суммирование распространяется на все значения
под знаком суммы указывает, что суммирование распространяется на все значения ![]() , меньшие
, меньшие ![]() .
.
Дифференциальная функция распределения
Непрерывную случайную величину можно задавать не только с помощью интегральной функции, но и с использованием дифференциальной функции распределения вероятностей.
Определение. Дифференциальной функцией распределения ![]() называется производная от интегральной функции:
называется производная от интегральной функции:
![]() .
.
Часто вместо термина «дифференциальная функция» пользуются термином «дифференциальный закон распределения» или термином «плотность вероятности».
Так как интегральная функция является первообразной дифференциальной функции, то вероятность того, что непрерывная случайная величина ![]() примет значение, принадлежащее интервалу
примет значение, принадлежащее интервалу ![]() , определяется равенством:
, определяется равенством: 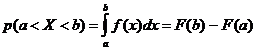 . Если известна дифференциальная функция, можно найти интегральную функцию распределения:
. Если известна дифференциальная функция, можно найти интегральную функцию распределения: 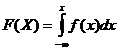 .
.
Свойства дифференциальной функции распределения
1. Дифференциальная функция распределения есть функция неотрицательная: ![]() .
.
2. Несобственный интеграл от дифференциальной функции распределения равен ![]()
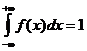 .
.
Последнее равенство называется условием нормировки плотности вероятностей.
Непрерывная случайная величина
Определение. Случайная величина ![]() называется непрерывной, если все её возможные значения полностью заполняют какой-либо конечный или бесконечный интервал числовой оси.
называется непрерывной, если все её возможные значения полностью заполняют какой-либо конечный или бесконечный интервал числовой оси.
Числовые характеристики непрерывной случайной величины
Математическое ожидание
Определение. Математическим ожиданием непрерывной случайной величины ![]() , возможные значения которой принадлежат отрезку
, возможные значения которой принадлежат отрезку ![]() , называется определённый интеграл:
, называется определённый интеграл:
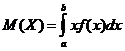 ,
,
где ![]() – плотность вероятности случайной величины
– плотность вероятности случайной величины ![]() .
.
Если возможные значения ![]() принадлежат всей числовой оси
принадлежат всей числовой оси ![]() , то
, то
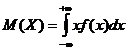 .
.
Все свойства математического ожидания дискретной случайной величины имеют силу и для непрерывной случайной величины.
Дисперсия
Определение. Дисперсией непрерывной случайной величины ![]() называется математическое ожидание квадрата отклонения этой величины от ее математического ожидания:
называется математическое ожидание квадрата отклонения этой величины от ее математического ожидания:
![]() .
.
Отсюда следует, что если возможные значения случайной величины принадлежат отрезку ![]() , то дисперсия
, то дисперсия
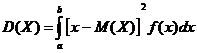 .
.
С учётом того, что для вычисления дисперсии справедлива формула
![]() , то
, то
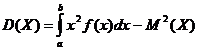 .
.
Если возможные значения ![]() принадлежат всей оси
принадлежат всей оси ![]() , то
, то
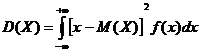 или
или
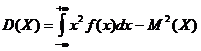 .
.
Среднеквадратическое отклонение
Среднеквадратическое отклонение непрерывной случайной величины определяется точно так же, как и для дискретной случайной величины:
![]()
Нормальное распределение непрерывной случайной величины (закон Гаусса)
Определение 1. Распределение вероятностей непрерывной случайной величины ![]() называется нормальным, если плотность вероятности описывается формулой:
называется нормальным, если плотность вероятности описывается формулой:
![]()
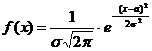 ,
,
![]() где
где ![]() – математическое ожидание нормально распределенной случайной величины,
– математическое ожидание нормально распределенной случайной величины,
![]() – среднеквадратическое отклонение нормального распределения.
– среднеквадратическое отклонение нормального распределения.
Закон Гаусса имеет большое значение для практического применения по следующим причинам:
1. На практике многие случайные величины оказываются либо нормально распределёнными, либо с распределениями, близкими к нормальному.
2. Случайную величину, не распределённую нормально, часто можно преобразовать таким образом, чтобы она имела распределение, близкое к нормальному.
3. Нормальное распределение может служить аппроксимацией для других распределений, например, для биноминального распределения.
4. При проверке статистических гипотез часто возникают распределения, которые оказываются нормальными.
Вычисление вероятности при нормальном распределении случайной величины
1. Вероятность попадания в интервал ![]() определяется формулой:
определяется формулой:
![]() ;
;
2. Вероятность попадания в интервал ![]() находим по формуле:
находим по формуле:
![]() , или
, или ![]() ;
;
3. Вероятность попадания в интервал ![]() находим по формуле:
находим по формуле:
![]() или
или ![]() ;
;
4. Вероятность того, что отклонение нормально распределенной случайной величины Х от математического ожидания ![]() по абсолютной величине меньше заданного положительного числа
по абсолютной величине меньше заданного положительного числа ![]() равна
равна ![]() ,
,
где 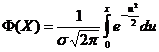 – функция Лапласа (Приложение 2),
– функция Лапласа (Приложение 2), ![]() математическое ожидание,
математическое ожидание, ![]() среднеквадратическое отклонение.
среднеквадратическое отклонение.
Примеры решения задач:
Задача 1. Задан закон распределения дискретной случайной величины ![]() :
:
X | 10 | 30 | 50 | 70 | 90 |
p | 0,1 | 0,2 | 0,1 | 0,2 | 0,4 |
Найти:
а) математическое ожидание ![]() , дисперсию
, дисперсию ![]() и среднеквадратическое отклонение
и среднеквадратическое отклонение ![]() ;
;

|
Из за большого объема этот материал размещен на нескольких страницах:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 |
 Основные порталы (построено редакторами)
Основные порталы (построено редакторами)

