Временной ряд называют детерминированным, если существует строгое функциональное соответствие между значениями времени регистрации и соответствующими значениями временного ряда. В этом случае значения временного ряда в любой фиксированный момент времени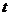 
строго определены соответствующей функцией 
.
Основные задачи анализа временных рядов:
– выделение и анализ основных составляющих временного ряда (тренда, сезонных, циклических и случайных компонентов);
– построение математических моделей временного ряда и проверка их адекватности;
– выявление связей между значениями одного или нескольких временных рядов;
– прогнозирование изменения изучаемого процесса на основе анализа его временного ряда.
Определение тренда
Основная тенденция изменения временного ряда, являющаяся долгосрочной составляющей и определяющая общее его изменение, называется трендом.
Изучение тренда состоит из двух этапов: определение наличия тренда и выделение тренда.
Для определения наличия тренда можно использовать критерий Стьюдента, который позволяет выявить различие выборочных средних половинок временного ряда. Если различие значимо, то подтверждается гипотеза о наличии тренда.
На практике часто возникает необходимость выявления основной тенденции изменения временного ряда (называемой трендом временного ряда), т. е. нахождения функции 
.
Решение подобной задачи существенно упрощается, если имеются определенные предположения (например, теоретические) относительно вида этой функции.
В тех случаях, когда функция является линейной, тренд временного ряда удобно представить следующим образом:
,
причем коэффициент 
и 
можно определить, используя метод наименьших квадратов.
Для определения значений а и b, необходимо решить систему двух уравнений:
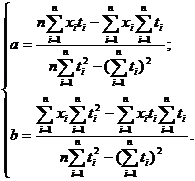
Пример решения задач:
Задача. Данные о динамике роста объема производства некоторого препарата на фармацевтической фабрике за 9 последовательных лет представлены в таблице:
Год | 2006 | 2007 | 2008 | 2009 | 2010 | 2011 | 2012 | 2013 | 2014 |
| 20 | 27 | 30 | 41 | 45 | 51 | 51 | 55 | 61 |
1) методом скользящего среднего провести сглаживание временного ряда;
2) построить линейную модель, параметры которой оценить МНК;
3) построить точечный прогноз на два шага вперед;
4) отобразить на графике фактические (экспериментальные) данные, результаты расчетов и прогнозирования;
Вычисления провести с точностью до сотых. Результаты промежуточных вычислений представить в таблицах.
Решение:
Так как рассматриваемая функция не зависит от даты, то данный ряд можно записать в следующем виде:
t | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
x | 20 | 27 | 30 | 41 | 45 | 51 | 51 | 55 | 61 |
1. Проведем сглаживание временного ряда:
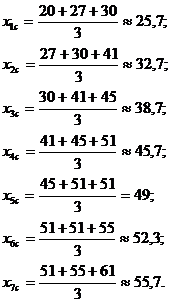
t | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 25,7 | 32,7 | 38,7 | 45,7 | 49 | 52,3 | 55,7 |
2. Найдем уравнение тренда в виде: 
Промежуточные вычисления выполним в таблице:
№ |
|
|
|
|
|
|
1 | 2 | 25,7 | 51,4 | 4 | 27,88 | 2,18 |
2 | 3 | 32,7 | 98,1 | 9 | 32,86 | 0,16 |
3 | 4 | 38,7 | 154,8 | 16 | 37,84 | -0,86 |
4 | 5 | 45,7 | 228,5 | 25 | 42,82 | -2,88 |
5 | 6 | 49 | 294 | 36 | 47,8 | -1,2 |
6 | 7 | 52,3 | 366,1 | 49 | 52,78 | 0,48 |
7 | 8 | 55,7 | 445,6 | 64 | 57,76 | 2,06 |
∑ | 35 | 299,8 | 1638,5 | 203 | -0,06 |
Коэффициенты и найдем по формулам:
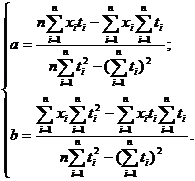
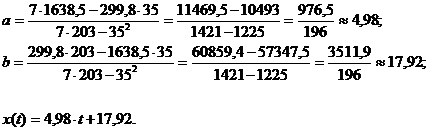
Вывод: так как Se близка к нулю, то найденная модель тренда адекватна данному процессу (хорошо описывает динамику роста объема производства некоторого препарата на фармацевтической фабрике).
3. Построим точный прогноз на два шага вперед, т. е. при t=9, t=10.
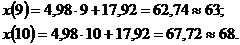
МАТЕМАТИЧЕСКИЕ МЕТОДЫ ТЕОРИИ ОПТИМИЗАЦИИ
(графический способ решения)
Математические методы оптимизации используют при решение таких практических задач, в которых требуется найти оптимальное из нескольких возможных решений.
При использовании данного метода решение задачи оптимизации в общем случае сводится к решению системы линейных алгебраических уравнений и неравенств.
Пример: Пусть задана система ограничений
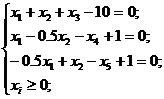
и целевая функция 
Требуется найти значения 
, удовлетворяющие данной системе и превращающие в минимум целевую функцию 
В нашем случае имеется 5 переменных и 3 уравнения, поэтому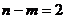 
переменных можно принять в качестве свободных, выразив через них базисные переменные.
Так как целевая функция содержит переменные 
и 
, то получим:
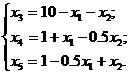
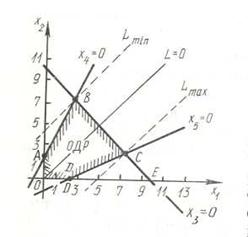
Каждая переменная в этой системе может принимать только неотрицательные значения. Геометрически это соответствует некоторой полуплоскости в системе координат 
рисунке.
Например, условие 
соответствует верхней полуплоскости, условие 
- правой, условие 
- полуплоскости, расположенной ниже прямой 
Действительно, при 
получим 
следовательно, начало координат лежит в полуплоскости, соответствующей положительным значениям переменной 
Построив далее прямые, соответствующие 
получим область в которой, в которой все переменные неотрицательны, т. е. область допустимых значений (на рисунке она заштрихована). Многоугольник, соответствующий области допустимых решений (ОДР), является выпуклым, поскольку представляет собой пересечение выпуклых областей, определяемых условиями 
|
Из за большого объема этот материал размещен на нескольких страницах:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 |
Основные порталы (построено редакторами)