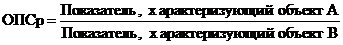Статистика (стр. 7 )

.

Например, известно, что на начало 1996 г. операции с ГКО проводили в Москве 108 официальных дилеров, в Новоси­бирске — 16 и в Санкт-Петербурге — 13. Таким образом, в Москве дилеров, которые проводили операции с ГКО, было в 6,8 раза больше, чем в Новосибирске и в 8,3 раза больше, чем в Санкт-Петербурге (или в Новосибирске было 14,8%, а в Санкт-Петербурге 12% от числа московских дилеров

Еще один вид относительных величин сравнения получают путем сопоставления индексов динамики разных явлений. В результате образуются индексы опережения или отставания в развитии одного явления по сравнению с другим. Так, если на предприятии производительность труда увеличилась на 12%, а средняя заработная плата только на 7,5%, то рост производительности труда опережает рост заработной платы по индексу изменения на 1 12: 107,5= 1,042, или на 4, 2%, а по темпу изменения на 12 : 7,5 = 1,6, или на 60%. Это и есть соответствующие индексы опережения. Индекс отставания роста заработной платы от роста производительности труда будет обратной величиной.

1.4.4. Понятие средних величин

Большое распространение в статистике имеют средние величины. Средние величины характеризуют качественные показатели коммерческой деятельности: издержки обращения, прибыль, рентабельность и др.

Средняя - это один из распространенных приемов обобщений. Правильное понимание сущности средней определяет ее особую значимость в условиях рыночной экономики, когда средняя через единичное и случайное позволяет выявить общее и необходимое, выявить тенденцию закономерностей экономического развития.

Средние величины - это обобщающие показатели, в которых находят выражение действия общих условий, закономерностей изучаемого явления.

Статистические средние рассчитываются на основе массовых данных правильно статистически организованного массового наблюдения (сплошного и выборочного). Однако статистическая средняя будет объективна и типична, если она рассчитывается по массовым данным для качественно однородной совокупности (массовых явлений). Например, если рассчитывать среднюю заработную плату в кооперативах и на госпредприятиях, а результат распространить на всю совокупность, то средняя фиктивна, так как рассчитана по неоднородной совокупности, и такая средняя теряет всякий смысл.

При помощи средней происходит как бы сглаживание различий в величине признака, которые возникают по тем или иным причинам у отдельных единиц наблюдения.

Например, средняя выработка продавца зависит от многих причин: квалификации, стажа, возраста, формы обслуживания, здоровья и т. д.

Средняя выработка отражает общее свойство всей совокупности.

Средняя величина является отражением значений изучаемого признака, следовательно, измеряется в той же размерности, что и этот признак.

Каждая средняя величина характеризует изучаемую совокупность по какому-либо одному признаку. Чтобы получить полное и всестороннее представление об изучаемой совокупности по ряду существенных признаков, в целом необходимо располагать системой средних величин, которые могут описать явление с разных сторон.

Существуют различные средние:

*  средняя арифметическая;

*  средняя геометрическая;

*  средняя гармоническая;

*  средняя квадратическая;

*  средняя хронологическая.

Рассмотрим некоторые виды средних, которые наиболее часто используются в статистике.

1.4.5. Средняя арифметическая

Средняя арифметическая простая (невзвешенная) равна сумме отдельных значений признака, деленной на число этих значений.

Отдельные значения признака называют вариантами и обозначают через х ( ); число единиц совокупности обозначают через n, среднее значение признака - через . Следовательно, средняя арифметическая простая равна:

Пример 1.

Имеются следующие данные о производстве рабочими продукции А за смену:

В данном примере варьирующий признак - выпуск продукции за смену.

Численные значения признака (16, 17 и т. д.) называют вариантами. Определим среднюю выработку продукции рабочими данной группы:

Простая средняя арифметическая применяется в случаях, когда имеются отдельные значения признака, т. е. данные не сгруппированы. Если данные представлены в виде рядов распределения или группировок, то средняя исчисляется иначе.

Пример 2.

Имеются следующие данные о заработной плате рабочих - сдельщиков:

Таблица 5.1.

По данным дискретного ряда распределения видно, что одни и те же значения признака (варианты) повторяются несколько раз.

Число одинаковых значений признака в рядах распределения называется частотой или весом и обозначается символом f.

Вычислим среднюю заработную плату одного рабочего в руб.:

Фонд заработной платы по каждой группе рабочих равен произведению варианты на частоту, а сумма этих произведений дает общий фонд заработной платы всех рабочих.

В соответствии с этим, расчеты можно представить в общем виде:

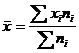
Полученная формула называется средней арифметической взвешенной.

Из нее видно, что средняя зависит не только от значений признака, но и от их частот, т. е. от состава совокупности, от ее структуры. Изменим в условии задачи состав рабочих и исчислим среднюю в измененной структуре.

Статистический материал в результате обработки может быть представлен не только в виде дискретных рядов распределения, но и в виде интервальных вариационных рядов с закрытыми или открытыми интервалами.

Рассмотрим расчет средней арифметической для таких рядов.

Пример 3.

Имеются следующие данные:

Таблица 5.2.

Исчислим среднюю выработку продукции одним рабочим за смену. В данном ряду варианты усредняемого признака (продукция за смену) представлены не одним числом, а в виде интервала "от - до". Рабочие первой группы производят продукцию от 3 до 5 шт., рабочие второй группы - от 5 до 7 шт. и т. д. Таким образом, каждая группа ряда распределения имеет нижнее и верхнее значения вариант, или закрытые интервалы. Исчисление средней по сгруппированным данным производится по формуле средней арифметической взвешенной:

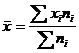
Чтобы применить эту формулу, необходимо варианты признака выразить одним числом (дискретным). За такое дискретное число принимается средняя арифметическая простая из верхнего и нижнего значения интервала. Так, для первой группы дискретная величина х будет равна: (3 + 5) / 2 = 4.

Дальнейший расчет производится обычным методом определения средней арифметической взвешенной:

Итак, все рабочие произвели 750 шт. изделий за смену, а каждый в среднем произвел 7,5 шт.

Преобразуем рассмотренный выше ряд распределения в ряд с открытыми интервалами.

Пример 4.

Имеются следующие данные о производстве продукции за смену:

Таблица 5.3.

В таких рядах условно величина интервала первой группы принимается равной величине интервала последующей, а величина интервала последней группы - величине интервала предыдущей. Дальнейший расчет аналогичен изложенному выше.

Из за большого объема этот материал размещен на нескольких страницах: 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49