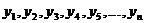Статистика (стр. 19 )

— исходные или фактические уровни ряда динамики заменяются средними уровнями:

...

...

...

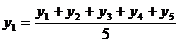
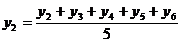
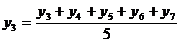
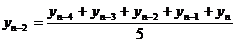
В результате получается сглаженный ряд, состоящий из скользящих пятизвенных средних уровней 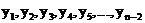. Между расположением уровней и устанавливается соответствие:

— — — — ,

сглаженный ряд короче исходного на число уровней , где k - число уровней, выбранных для определения средних уровней ряда.

Сглаживание методом скользящих средних можно производить по четырём, пяти или другому числу уровней ряда, используя соответствующие формулы для усреднения исходных уровней.

Полученные при этом средние уровни называются четырёхзвенными скользящими средними, пятизвенными скользящими средними и т. д.

При сглаживании ряда динамики по чётному числу уровней выполняется дополнительная операция, называемая центрированием, поскольку, при вычислении скользящего среднего, например по четырём уровням, относится к временной точке между моментами времени, когда были зафиксированы фактические уровни и . Схема вычислений и расположений уровней сглаженного ряда становится сложнее:

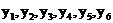... — исходные уровни;

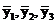— — ... — сглаженные уровни;

— — ... — центрированные сглаженные уровни;

.

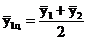
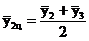Метод скользящих средних не позволяет получить численные оценки для выражения основной тенденции в ряду динамики, давая лишь наглядное графическое представление (пример 1).

Пример.

Таблица 1.

На рис. 1 показан график, построенный по данным о валовом сборе хлопка-сырца в стране за ряд лет наблюдения и по расчетным данным, представленным в таблице 1.

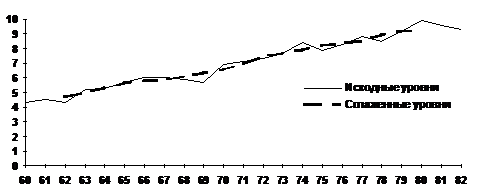
Рис. 1. Валовый сбор хлопка - сырца

Наиболее совершенным способом определения тенденции развития в ряду динамики является метод аналитического выравнивания. При этом методе исходные уровни ряда динамики заменяются теоретическими или расчетными , которые представляют из себя некоторую достаточно простую математическую функцию времени, выражающую общую тенденцию развития ряда динамики. Чаще всего в качестве такой функции выбирают прямую, параболу, экспоненту и др.

Например, ,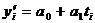

где - коэффициенты, определяемые в методе аналитического выравнивания;

- моменты времени, для которых были получены исходные и соответствующие теоретические уровни ряда динамики, образующие прямую, определяемую коэффициентами .

Расчет коэффициентов ведется на основе метода наименьших квадратов:

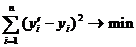
Если вместо подставить 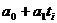(или соответствующее выражение для других математических функций), получим:

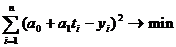
Это функция двух переменных (все и известны), которая при определенных достигает минимума. Из этого выражения на основе знаний, полученных в курсе высшей математики об экстремуме функций n переменных, получают значения коэффициентов .

Для прямой:

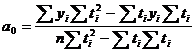
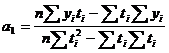
где n — число моментов времени, для которых были получены исходные уровни ряда .

Если вместо абсолютного времени выбрать условное время таким образом, чтобы , то записанные выражения для определения упрощаются:

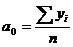
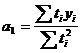
Пример.

Нечетное число уровня ряда.

Чётное число уровней ряда.

В обоих случаях .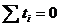

Пример.

Выполняется аналитическое выравнивание ряда, отражающего производство стали в стране по годам (млн. т).

В качестве математической функции, отражающей тенденцию развития, выбирается прямая , определение производится для условного времени, в результате , .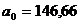

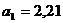Из за большого объема этот материал размещен на нескольких страницах: 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49