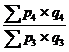Индекс цен американского экономиста И. Фишера представляет собой среднюю геометрическую из произведений двух агрегатных индексов цен Ласпейреса и Пааше:
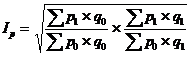 .
.
Геометрическая форма индексов имеет большой недостаток - она лишена конкретного экономического содержания. Так, в отличие от агрегатных индексов разность между числителем и знаменателем не покажет никакой реальной экономии (или потерь) из-за изменения цен или физического объема продукции. Индекс Фишера целесообразно использовать для исчисления индексов цен за длительный период времени для сглаживания тенденций в структуре и составе объема продукции.
Для пересчета стоимостных показателей из текущих цен в сопоставимые используется индекс-дефлятор, который является агрегированной формой индекса цен. Дефлятор - это коэффициент, переводящий значение стоимостного показателя за отчетный период в стоимостные измерители базисного. Индекс-дефлятор рассчитывается как отношение фактической стоимости продукции отчетного периода к стоимости объема продукции, структура которого аналогична структуре отчетного периода, но определенного в ценах базисного года. В основе расчета индекса-дефлятора лежит формула Пааше - агрегатная формула индекса цен с текущими весами. Важной особенностью индекса-дефлятора является то, что он не может быть использован для сравнительной оценки динамики цен за два периода. Индексы-дефляторы дают представление только об отношении стоимости продукции в текущем периоде к ее стоимости в базисном периоде без учета отличия состава и структуры продукции.
1.9.4. Цепные и базисные индексы
Для изучения динамики явления за ряд периодов возможно вычисление системы цепных и базисных индексов. Построение такой системы возможно в двух вариантах:
1. Оценивают относительное изменение уровня изучаемого явления по сравнению с каким-то одним определенным периодом времени. В этом случае строится система индексов с постоянной базой сравнения, то есть базисные индексы.
2. Оценивают относительное изменение уровня изучаемого явления по сравнению с предшествующим периодом. В этом случае строится система индексов с переменной базой сравнения, то есть цепные индексы.
Рассмотрим системы цепных и базисных индексов цен, физического объема продукции и стоимости продукции.
Индексы | Базисные индексы | Цепные индексы |
Индивидуальные индексы физического объема |
|
|
Агрегатные индексы физического объема |
|
|
Индивидуальные индексы цен |
|
|
Агрегатные индексы цен |
|
|
Индивидуальные индексы стоимости |
|
|
Агрегатные индексы стоимости |
|
|
При исчислении индексов физического объема может быть применена другая система весов. Например, при исчислении отдельных индексов используются цены периода, предшествующего отчетному. Тогда получают следующий ряд цепных индексов:
J1/0=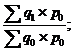 J2/1=
J2/1=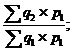 J3/2=
J3/2=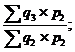 J4/3=
J4/3=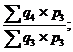
Для индивидуальных индексов цен, физического объема и стоимости справедливо следующее правило:
1. Произведение промежуточных по периодам цепных индексов дает базисный индекс последнего периода i4/0=i1/0![]() i2/1
i2/1![]() i3/2
i3/2![]() i3/4
i3/4
2. Отношение базисного индекса отчетного периода к базисному индексу предшествующего периода дает цепной индекс отчетного периода i3/4=i4/0:i3/0
Это правило позволяет применять так называемый цепной метод, то есть находить неизвестный ряд базисных индексов по известным цепным и обратно.
Имея два базисных агрегатных индекса физического объема с постоянным соизмерителем, можно получить цепной индекс отчетного периода.
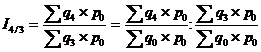
Базисный индекс отчетного периода может быть получен перемножением соответствующих цепных индексов, если соизмеритель принимается на уровне одного и того же периода:
I4/0= I1/0![]() I 2/1
I 2/1![]() I3/2
I3/2![]() I4/3
I4/3
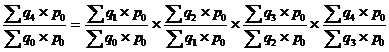
При использовании переменных соизмерителей цепной метод применять нельзя, так как цепные индексы в этом случае несопоставимы друг с другом.
Агрегатные индексы качественных показателей всегда являются индексами с переменными весами, так как соизмеритель всегда принимается на уровне отчетного периода. Поэтому цепной метод расчета индексов не применим к агрегатным индексам качественных показателей.
Сформулированное выше правило взаимосвязи цепных и базисных индексов в полном объеме применимо к агрегатным индексам стоимости.
Рассмотрим на примере расчет базисных и цепных индексов и проверим их взаимосвязь.
Вид про- дукции | Произведено продукции, т ( q ) | Сопоста- вимая цена за 1 т, млн. руб. | ||||
1992 г. | 1993 г. | 1994 г. | 1995 г. | 1996 г. | ( р0 ) | |
1. | 1000 | 1050 | 1102 | 1158 | 1219 | 100 |
2. | 500 | 550 | 600 | 650 | 700 | 200 |
Во-первых, рассчитаем базисные (в % к 1992 г.) и цепные индексы физического объема каждого вида и всей продукции.
Базисные индексы:
Индексы | По продукции № 1 | По продукции № 2 | По двум видам продукции в целом |
1993 г. к 1992 г. | 1050 : 1000 = 1,05 | 550 : 500 = 1,1 | (1050 200):(1000 500 |
1994 г. к 1992 г. | 1102 : 1000 = 1,1 | 600 : 500 = 1,2 | (1102 200): 200000 = 1,15 |
1995 г. к 1992 г. | 1158 : 1000 = 1,16 | 650 : 500 = 1,3 | (1158 200): 200000 = 1,23 |
1996 г. к 1992 г. | 1219 : 1000 = 1,21 | 700 : 500 = 1,4 | (1219 200):200000= 1,31 |
Цепные индексы:

|
Из за большого объема этот материал размещен на нескольких страницах:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 |



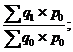
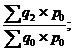
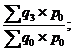
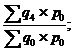
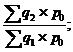
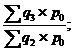
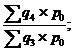
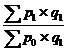 ;
;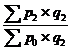
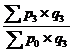 ;
;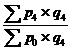
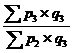 ;
; 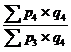
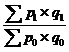 ;
;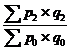 ;
;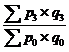 ;
; 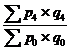
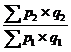 ;
;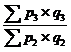 ;
;