Индексы | По продукции № 1 | По продукции № 2 | По двум видам продукции в целом |
1993 г. к 1992 г. | 1050 : 1000 = 1,050 | 550 : 500 = 1,1 | (1050 200):(1000 500 |
1994 г. к 1993 г. | 1102 : 1050 = 1,049 | 600 : 550 = 1.091 | (1102 200):(1050 550 |
1995 г. к 1994 г. | 1158 : 1102 = 1,051 | 650 : 600 = 1,083 | (1158 200):(1102 600 |
1996 г. к 1995 г. | 1219 : 1158 = 1,053 | 700 : 650 = 1,077 | (2119 200):(1158 650 |
Во-вторых, проверим взаимосвязь исчисленных базисных и цепных индексов физического объема продукции:
а) произведение промежуточных по периодам цепных индексов дает базисный индекс последнего периода
I 96/92 = I93/92
I94/93 I 95/94I96/95
1,31 = 1,08 1,071 1,068 1,066
б) отношение базисного индекса отчетного периода к базисному индексу предшествующего периода дает цепной индекс отчетного периода
I 96/95 = I 96/95 : I 95/92
1,066 = 1,31 : 1,23
1.9.5. Использование индексов в экономическом анализе
Агрегатные индексы применяются для характеристики изменения уровня сложных общественных явлений. Их можно применять в аналитических целях для оценки влияния на объемный показатель изменения факторов его формирующих. Предпосылкой для проведения анализа в индексной форме является возможность представить результативный экономический показатель произведением двух и более определяющих его величину факторов или суммой таких произведений.
Оценивать роль отдельных факторов изменения явления статистика может путем построения системы взаимосвязанных индексов. Задача состоит в том, чтобы рассчитать изменение сложного показателя при изменении величины только одного фактора так, чтобы величина других факторов была бы сохранена на определенном постоянном уровне. В основе аналитических индексных расчетов лежит принцип измерения изменений величины всех факторов, кроме изучаемого. При построении индексов, оценивающих влияние отдельных факторов на изменение сложного явления, следует иметь в виду, что общий результат изменения этого явления представляет собой сумму изменений за счет влияния всех исследуемых факторов, формирующих это явление.
Рассмотрим разложение прироста сложного показателя по факторам, когда этот показатель представлен в виде произведения двух множителей (факторов).
Номер предприятия | Выработано продукции, тыс. штук | Отработано человеко-дней, тысяч | ||
отчетный год | базисный год | отчетный год | ||
1. | 20000 | 34000 | 100 | 136 |
2. | 5000 | 6000 | 50 | 54 |
Итого | 25000 | 40000 | 150 | 190 |
Исходя из того, что производительность труда можно представить как отношение количества выработанной продукции за определенный период времени к числу отработанных человеко-дней, на основе имеющейся информации рассчитаем следующие показатели и проанализируем их взаимосвязь:
1. Относительное изменение производительности труда по группе предприятий в отчетном периоде по сравнению с базисным в целом и за счет отдельных факторов. Для расчета этого показателя необходимо вычислить индексы динамики производительности труда переменного и постоянного состава, а также индекс структурных сдвигов.
Общее изменение среднего уровня производительности труда по группе предприятий покажет индекс переменного состава, исчисленный по следующей формуле:
=
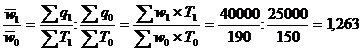
Изменение среднего уровня производительности труда по группе предприятий за счет роста производительности труда на отдельных предприятиях отражает индекс постоянного состава, рассчитанный по формуле:
= 
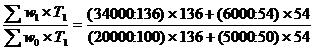=1,227
Изменение среднего уровня производительности труда по группе предприятий за счет изменения в соотношении количества отработанных человеко-дней на отдельных предприятиях выявит индекс структурных сдвигов, вычисленный по формуле:
Id =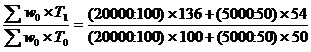 
= 1,029
Взаимосвязь исчисленных индексов выражает следующее уравнение:
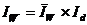
1,263 = 1,227 1,029
В отчетном периоде по сравнению с базисным производительность труда по группе предприятий возросла в среднем на 26,3 %, в том числе за счет роста производительности труда на отдельных предприятиях - на 22,7 % и за счет изменения структуры отработанного времени - на 2,9 %.
2. Абсолютный изменение объема производства продукции в отчетном периоде по сравнению с базисным в целом и за счет отдельных факторов рассчитаем по следующей схеме:
а) абсолютный прирост объема продукции в отчетном периоде по сравнению с базисным составит 15000 тыс. штук
q =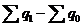 
= 40000 - 25000
б) прирост объема продукции в отчетном периоде по сравнению с базисным за счет качественного фактора (производительности труда) равен приросту этого фактора, умноженному на отчетный уровень количественного фактора ( отработанное время)
=(40000:190-25000:150)190 = 8322 тыс. руб.
в) прирост объема продукции в отчетном периоде по сравнению с базисным за счет количественного фактора (отработанного времени) равен приросту этого фактора, умноженному на базисный уровень качественного фактора (производительность труда)
(190 - 150) (25000 : 150) = 6668 тыс. руб.
В отчетном периоде по сравнению с базисным объем произведенной продукции увеличился на 15000 тыс. рублей, в том числе за счет изменения среднего уровня производительности труда по группе предприятий - на 8322 тыс. рублей и количества отработанного времени - на 6668 тыс. рублей.
При проведении экономического анализа часто возникает необходимость построения многофакторных индексных моделей. Рассмотрим на примере разложение прироста сложного показателя по факторам, который может быть представлен в виде трех множителей (факторов).
Показатели (факторы) | Базисный период | Отчетный период |
Число отделений банка (c) | 20 | 25 |
Среднее число вкладчиков в отделениях банка (b) | 2900 | 3600 |
Средний размер вклада, тыс. рублей (a) | 6000 | 7000 |
Среднюю сумму вкладов (s), привлеченную отделениями банка, можно рассчитать как произведение среднего размера вклада, среднего числа вкладчиков в отделениях банка и числа отделений банка. Взаимосвязь этих показателей может быть выражена в виде трехфакторной индексной модели:
|
Из за большого объема этот материал размещен на нескольких страницах:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 |
