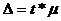.

При этом t как коэффициент кратности средней ошибки выборки зависит от значения вероятности Р, с которой гарантируется величина предельной ошибки выборки.

Предельная ошибка выборки при бесповторном отборе определяется по следующим формулам:

, .

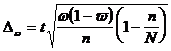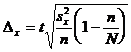Предельная ошибка выборки при повторном отборе определяется по формуле:

, .

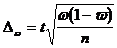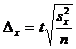1.6.3. Малая выборка

При контроле качества товаров в экономических исследованиях эксперимент может проводиться на основе малой выборки.

Под малой выборкой понимается несплошное статистическое обследование, при котором выборочная совокупность образуется из сравнительно небольшого числа единиц генеральной совокупности. Объем малой выборки обычно не превышает 30 единиц и может доходить до 4 — 5 единиц.

Средняя ошибка малой выборки вычисляется по формуле:

,

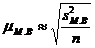где — дисперсия малой выборки.

При определении дисперсии число степеней свободы равно n-1:

.

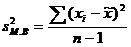Предельная ошибка малой выборки определяется по формуле

При этом значение коэффициента доверия t зависит не только от заданной доверительной вероятности, но и от численности единиц выборки n. Для отдельных значений t и n доверительная вероятность малой выборки определяется по специальным таблицам Стьюдента (Табл. 6.1.), в которых даны распределения стандартизированных отклонений:

.

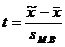Таблица 6.1

n

t

0,5

1,0

1,5

2,0

3,0

4

0,347

0,609

0,769

0,861

0,942

6

0,362

0,637

0,806

0,898

0,970

8

0,368

0,649

0,823

0,914

0,980

10

0,371

0,657

0,832

0,923

0,985

15

0,376

0,666

0,846

0,936

0,992

20

0,377

0,670

0,850

0,940

0,993

Поскольку при проведении малой выборки в качестве доверительной вероятности практически принимается значение 0,59 или 0,99, то для определения предельной ошибки малой выборки используются следующие показания распределения Стьюдента (Табл. 6.2.)

Таблица 6.2

n

0,95

0,99

4

3,183

5,841

5

2,777

4,604

6

2,571

4,032

7

2,447

3,707

8

2,364

3,500

9

2,307

3,356

10

2,263

3,250

15

2,119

2,921

20

2,078

2,832

Пример.

При контрольной проверке качества поставленной в торговлю колбасы получены данные о содержании поваренной соли в пробах. По данным выборочного обследования нужно установить с вероятностью 0,95 предел, в котором находится средний процент содержания поваренной соли в данной партии товара.

Составляем расчётную таблицу и по её итогам определяем среднюю пробу малой выборки.

Таблица 6.3

Пробы

4,3

0,2

0,04

4,2

0,1

0,01

3,8

0,3

0,09

4,3

0,2

0,04

3,7

- 0,4

0,16

3,9

- 0,2

0,04

4,5

0,4

0,16

4,4

0,3

0,09

4,0

- 0,1

0,01

3,9

- 0,2

0,04

41,0

—

0,68

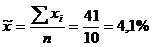
Определяем дисперсию малой выборки:

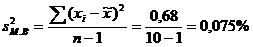
Определяем среднюю ошибку малой выборки:

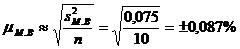
Исходя из численности выборки (n=10) и заданной вероятности =0,95, устанавливается по распределению Стьюдента (см. Табл. 6.2.) значение коэффициента доверия t=2,263.

Предельная ошибка малой выборки составит:

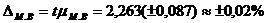
Следовательно, с вероятностью 0,95 можно утверждать, что во всей партии колбасы содержание поваренной соли находится в пределах:

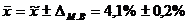, т. е. от 4,1% - 0,2%=3,9%

до 4,1%+0,2%=4,3%.

1.6.4. Способы распространения характеристик выборки на генеральную совокупность

Выборочный метод чаще всего применяется для получения характеристик генеральной совокупности по соответствующим показателям выборки. В зависимости от целей исследований это осуществляется или прямым пересчётом показателей выборки для генеральной совокупности, или посредством расчёта поправочных коэффициентов.

Способ прямого пересчёта. Он состоит в том, что показатели выборочной доли или средней распространяется на генеральную совокупность с учётом ошибки выборки.

Так, в торговле определяется количество поступивших в партии товара нестандартных изделий. Для этого (с учётом принятой степени вероятности) показатели доли нестандартных изделий в выборке умножаются на численность изделий во всей партии товара.

Пример.

При выборочном обследовании партии нарезных батонов 2 000 ед. доля нестандартных изделий в выборке составляет: 0,1 (10 : 100) при установленной с вероятностью =0,954 предельной ошибке выборки .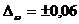

На основе этих данных доля нестандартных изделий во всей партии составит: или от 0,04 до 0,16.

Способом прямого пересчёта можно определить пределы абсолютной численности нестандартных изделий во всей партии: минимальная численность — 2 000 : 0,04 = 80 шт.; максимальная численность — 2 000 : 0,16 = 320 шт.

Способ поправочных коэффициентов. Применяется в случаях, когда целью выборочного метода является уточнение результатов сплошного учета.

В статистической практике этот способ используется при уточнении данных ежегодных переписей скота, находящегося у населения. Для этого после обобщения данных сплошного учета практикуется 10%-ное выборочное обследование с определением так называемого “процента недоучета”.

Так, например, если в хозяйствах населения поселка по данным 10%-ной выборки было зарегистрировано 52 головы скота, а по данным сплошного учета в этом массиве значится 50 голов, то коэффициент недоучета составляет 4% [(2*50):100]. С учетом полученного коэффициента вносится поправка в общую численность скота, находящегося у населения данного поселка.

1.6.5. Способы отбора единиц из генеральной совокупности

Из за большого объема этот материал размещен на нескольких страницах:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49