Статистика (стр. 11 )

Исчислим дисперсию: .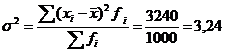

Техника вычисления дисперсии сложна, а при больших значениях вариант и частот может быть громоздкой. Расчеты можно упростить, используя свойства дисперсии.

Свойства дисперсии.

  Уменьшение или увеличение весов (частот) варьирующего признака в определенное число раз дисперсии не изменяет.

  Уменьшение или увеличение каждого значения признака на одну и ту же постоянную величину А дисперсии не изменяет.

  Уменьшение или увеличение каждого значения признака в какое-то число k раз соответственно уменьшает или увеличивает дисперсию в раз, а среднее квадратическое отклонение - в k раз.

  Дисперсия признака относительно произвольной величины всегда больше дисперсии относительно средней арифметической на квадрат разности между средней и произвольной величиной: . Если А равна нулю, то приходим к следующему равенству: 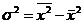, т. е. дисперсия признака равна разности между средним квадратом значений признака и квадратом средней.

Каждое свойство при расчете дисперсии может быть применено самостоятельно или в сочетании с другими.

Порядок расчета дисперсии простой:

1) определяют среднюю арифметическую ;

2) возводят в квадрат среднюю арифметическую;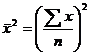

3) возводят в квадрат каждую варианту ряда ;

4) находим сумму квадратов вариант ;

5) делят сумму квадратов вариант на их число, т. е. определяют средний квадрат ;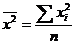

6) определяют разность между средним квадратом признака и квадратом средней .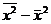

Пример 5.

Имеются следующие данные о производительности труда рабочих:

Таблица 5.5 - Данные о производительности труда рабочих

Произведем следующие расчеты: шт.

.

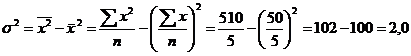Пример 6.

Определить дисперсию в дискретном ряду распределения, используя табл. 5.6.

Таблица 5.6 - Распределение рабочих по выпуску продукции

.

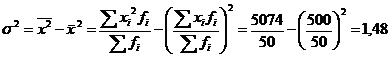Получим тот же результат, что в табл. 5.3.

Порядок расчета дисперсии взвешенной (по формуле ):

1)  определяют среднюю арифметическую ;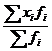

2)  возводят в квадрат полученную среднюю ;

3)  возводят в квадрат каждую варианту ряда ;

4)  умножают квадраты вариант на частоты ;

5)  суммируют полученные произведения ;

6)  делят полученную сумму на сумму весов и получают средний квадрат признака ;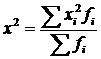

7)  определяют разность между средним значением квадратов и квадратом средней арифметической, т. е. дисперсию .

Пример 7.

Имеются следующие данные о распределении посевной площади колхоза по урожайности пшеницы:

Таблица 5.7 - Распределение посевной площади колхоза по урожайности пшеницы

В подобных примерах, прежде всего, определяется дискретное значение признака в каждом интервале, а затем применяется метод расчета, указанный выше:

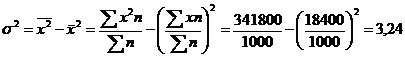
Заметим, что средняя величина отражает тенденцию развития, т. е. действие главных причин, а среднее квадратическое отклонение измеряет силу воздействия прочих факторов.

Для характеристики меры колеблемости изучаемого признака исчисляются показатели относительного рассеивания (колеблемости) в относительных величинах. Они позволяют сравнивать характер рассеивания в различных распределениях (различные единицы наблюдения одного и того же признака в двух совокупностях, при различных значениях средних, при сравнении разноименных совокупностей). Расчет показателей меры относительного рассеивания осуществляют как отношение абсолютного показателя рассеивания к средней арифметической, умножаемое на 100%.

1. Коэффициент осцилляции отражает относительную колеблемость крайних значений признака вокруг средней.

(1)

2. Относительное линейное отклонение характеризует долю усредненного значения абсолютных отклонений от средней величины.

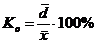(2)

3. Коэффициент вариации.

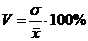(3)

Учитывая, что среднеквадратическое отклонение дает обобщающую характеристику колеблемости всех вариантов совокупности, коэффициент вариации является наиболее распространенным показателем колеблемости, используемым для оценки типичности средних величин. При этом исходят из того, что если V больше 33,3 %, то это говорит о большой колеблемости признака в изучаемой совокупности (иначе: исследуемая совокупность считается весьма неоднородной и для проведения дальнейшего исследования должна быть разгруппирована).

Если исследуемую совокупность единиц расчленить на группы, то можно считать, что общая дисперсия всей совокупности варьирует (изменяется) под влиянием дисперсий для каждой отдельной группы так называемых групповых или частных дисперсий и межгрупповой дисперсии. Эти дисперсии связаны между собой правилом сложения дисперсий. При использовании правила сложения дисперсий в экономическом анализе по величине частной дисперсии может решаться задача выявления наиболее эффективной в производстве системы (формы, структуры и т. п.) организации труда, его оплаты и т. д.

Правило сложений дисперсий для средней величины признака:

Из за большого объема этот материал размещен на нескольких страницах: 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49