Для февраля:

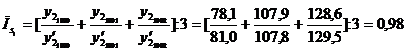
и т. д.

Индексы сезонности по месяцам сведены в таблицу:

Построив линейный график, можно увидеть закономерности изменения объёма продаж сахара по месяцам года.

Применение индексов дает нам возможность провести экономический анализ социально-экономических явлений в двух направлениях: синтетическом и аналитическом. Синтетическое направление определяет индекс как показатель среднего изменения уровня изучаемого явления. Аналитическое направление трактует индекс как показатель изменения уровня результативной величины под влиянием изменения индексируемой величины. Величина, изменение которой изучается в данном конкретном случае с помощью индекса, называется индексируемой величиной. Например, индекс физического объёма товарооборота фирмы (Iq) составил 115% или 1,15. Полученный результат можно интерпретировать следующим образом: на уровне синтетического анализа - физический объём товарооборота фирмы увеличился в отчетном периоде по сравнению с базисным на 15%; на уровне аналитического анализа - в результате роста количества проданных товаров товарооборот фирмы увеличился в отчетном периоде по сравнению с базисным на 15%.

Для удобства в теории статистики разработана определенная символика, в том числе для индексируемых величин. Так, количество единиц данного вида продукции (товаров) обозначается “q”, цена единицы продукции (товаров) - “p”, себестоимость единицы продукции - “z”, трудоемкость единицы изделия - “t”.

Способы построения индексов зависят от содержания изучаемых явлений, методологии расчета исходных статистических показателей и целей исследования. В основу классификации индексов можно положить следующие признаки: степень охвата элементов изучаемой совокупности, содержание и характер индексируемой величины, методология расчета.

По степени охвата элементов изучаемой совокупности различают: индивидуальные индексы и сводные индексы. Индивидуальный индекс - это относительный показатель, выражающий изменение отдельного элемента сложного экономического явления. Индивидуальный индекс обозначается буквой “i”. К индивидуальным индексам относятся показатели, характеризующие изменение количества произведенной продукции одного вида, соотношение цен одного товара, трудоемкости одного изделия и т. д. В числителе индивидуального индекса - величина индексируемой величины в текущем периоде, а в знаменателе - в базисном периоде. Например, индивидуальный индекс себестоимости продукции “А” во втором квартале 1997 года по сравнению с первым кварталом 1997 года равен отношению себестоимости изделия “А” во втором квартале - 650 тыс. рублей к себестоимости изделия “А” в первом квартале - 610 тыс. рублей.

iq = q1 : q0 = 650 : 610 100 = 106,5 %

Сводный индекс выражает соотношение величин сложного экономического явления, состоящего из элементов непосредственно несоизмеримых. Сводный индекс обозначается буквой “I”. Сводный индекс характеризует изменение во времени, по сравнению с планом или в пространстве объема разнородной продукции, цен на различные товары, себестоимости ряда изделий, производительности труда по группе предприятий и т. д. Для получения сводного индекса не может быть применено непосредственное суммирование таких несоизмеримых величин для каждого из сравниваемых периодов и последующее соотношение этих сумм. Расчет сводного индекса на основе простой средней из индивидуальных индексов также не может быть применен, так как в такой средней не учитывается удельный вес каждого элемента во всей совокупности изучаемого явления. Основной формулой для расчета сводного индекса является агрегатная формула, в которой с помощью весов индекса несоизмеримые величины приводятся к соизмеримому виду. Например, индекс физического объёма продукции можно рассчитать по следующей формуле:

Iq =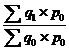

где q0 и q1 - количество продукции за базисный и отчетный периоды; р0 - веса индекса - неизменные цены базисного периода.

Сводные индексы можно разделить на групповые и общие. Групповой индекс рассчитывается для группы элементов, входящих в общую совокупность. Например, индекс цен для товаров, входящих в какую-либо товарную группу (молоко и молочные продукты, аудио - и видеотехника и т. д.).Групповые индексы рассчитываются по обычным формулам сводных индексов. Общий индекс рассчитывается для всей совокупности элементов изучаемого явления. Общий индекс иногда употребляется как синоним понятия сводного индекса.

В зависимости от содержания и характера индексируемой величины различают: индексы количественных (объемных) показателей и индексы качественных показателей. Например, индекс физического объёма товарооборота - это индекс количественного показателя, а индекс цен или индекс себестоимости продукции - это индексы качественных показателей.

Для выражения соотношения экономических явлений в пространстве ( по городам, регионам, странам и т. д.) используют территориальные индексы. При построении территориальных индексов особое значение приобретает вопрос о весах индекса. Например, при сравнении уровня себестоимости по двум регионам можно с равным правом выбрать в качестве веса количество произведенной продукции каждого региона. Различия индексов, рассчитанных с весами разных регионов, могут быть существенными. Поэтому к построению территориальных индексов необходим особый подход по сравнению с индексами, выражающими изменение явления во времени.

Территориальный индекс может быть получен сопоставлением уровня исследуемого явления по городу со средним уровнем этого явления для всей страны, региона и т. д. Другой способ построения территориальных индексов основан на непосредственном сопоставлении уровней явления с применением стандартизованных (одинаковых) весов, общих для всех регионов. В этом случае территориальный индекс себестоимости будет равен:

Iz = ,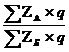

где zА и zБ - себестоимость произведенной продукции по видам в регионе “А” и в регионе “Б”, q - количество продукции данного вида, выработанное по всей стране или региону. Аналогично рассчитываются территориальные индексы для других качественных показателей.

При построении территориальных индексов для количественных показателей способ стандартизованных весов удобнее использовать в виде среднего арифметического индекса, в котором рассчитанные предварительно территориальные индексы для каждой отрасли экономики, взвешиваются затем по структуре отраслей страны или региона. Расчет можно произвести по формуле:

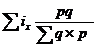
где ix - территориальный индекс для отрасли, полученный на основе соотношения продукции отрасли по регионам, - доля данной отрасли во всей продукции региона или страны.

В зависимости от методологии расчета различают: агрегатные индексы и средние индексы; цепные и базисные индексы.

Агрегатный индекс является формой сводного индекса, используемой для характеристики изменения сложного экономического явления. Числитель и знаменатель агрегатного индекса представляют собой суммы произведений индексируемых величин двух сравниваемых периодов (или фактических и плановых значений и т. д.) на некоторые одинаковые для обоих периодов величины, называемые весами агрегатных индексов. Агрегатный индекс является основной формой индекса, так как в этом индексе отчетливо выступает отношение двух абсолютных величин, различающихся за счет изменения изучаемого явления. В агрегатном индексе изменяется только индексируемая величина, а вес остается неизменным, тем самым его влияние на величину индекса элиминируется.

Из за большого объема этот материал размещен на нескольких страницах: 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49