При одноступенчатой выборке каждая отобранная единица сразу же подвергается изучению по заданному признаку. Так обстоит дело при собственно-случайной и серийной выборке.

При многоступенчатой выборке производят подбор из генеральной совокупности отдельных групп, а из групп выбираются отдельные единицы. Так производится типическая выборка с механическим способом отбора единиц в выборочную совокупность.

Комбинированная выборка может быть двухступенчатой. При этом генеральная совокупность сначала разбивается на группы. Затем производят отбор групп, а внутри последних осуществляется отбор отдельных единиц.

Балансовая связь — характеризует зависимость между источниками формирования ресурсов (средств) и их использованием.

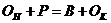
— остаток товаров на начало отчетного периода;

— поступление товаров за период;

— выбытие товаров в изучаемом периоде;

— остаток товаров на конец отчетного периода.

Левая часть формулы характеризует предложение товаров

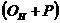, а правая часть — использование товарных ресурсов .

Компонентные связи показателей коммерческой деятельности характеризуются тем, что изменение статистического показателя определяется изменением компонентов, входящих в этот показатель, как множители:

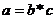
В статистике коммерческой деятельности компонентные связи используются в индексном методе. Например, индекс товарооборота в фактических ценах представляет произведение двух компонентов — индекса товарооборота в сопоставимых ценах и индекса цен , т. е.

.

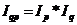Важное значение компонентной связи состоит в том, что она позволяет определять величину одного из неизвестных компонентов:

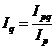или

Факторные связи характеризуются тем, что они проявляются в согласованной вариации изучаемых показателей. При этом одни показатели выступают как факторные, а другие — как результативные.

Факторные связи могут рассматриваться как функциональные и корреляционные.

При функциональной связи изменение результативного признака всецело зависит от изменения факторного признака :

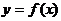
При корреляционной связи изменение результативного признака не всецело зависит от факторного признака , а лишь частично, так как возможно влияние прочих факторов :

.

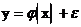Примером корреляционной связи показателей коммерческой деятельности является зависимость сумм издержек обращения от объема товарооборота. В этой связи, помимо факторного признака — объема товарооборота , на результативный признак (сумму издержек обращения ) влияют и другие факторы, в том числе и не учтенные . Поэтому корреляционные связи не являются полными (тесными) зависимостями.

Характерной особенностью корреляционных связей является то, что они проявляются не в единичных случаях, а в массе.

При статистическом изучении корреляционной связи показателей коммерческой деятельности перед статистикой ставятся следующие основные задачи:

1) проверка положений экономической теории о возможности связи между изучаемыми показателями и придание выявленной связи аналитической формы зависимости;

2) установление количественных оценок тесноты связи, характеризующих силу влияния факторных признаков на результативные.

Для того, чтобы установить, есть ли зависимость между величинами, используются многообразные статистические методы, позволяющие определить, во-первых — какие связи; во-вторых — тесноту связи (в одном случае она сильная, устойчивая, в другом — слабая); в-третьих — форму связи (т. е. формулу, связывающую величину и).

В процессе изучения связи надо учитывать, что мы используем математический аппарат, но всегда надо иметь теоретические обоснования той связи, которую пытаются показать.

1.7.2. Методы изучения статистической связи

Наиболее простой способ иллюстрации зависимости между двумя величинами — построение таблиц, показывающих, как при изменении одной величины меняется другая.

Пример.

Таблица показывает лишь согласованность в изменении двух величин, наличие связи. Но она не определяет ни тесноту связи, ни форму этой связи.

Для того, чтобы ответить на эти вопросы, необходимо использовать специальные статистические методы. Среди них есть очень простые и менее точные, более сложные и более точные. Но все они имеют один и тот же смысл.

Один из простых показателей тесноты корреляционной зависимости — показатель корреляции рангов. Разберем порядок вычисления этого показателя на примере.

Изучается товарооборот и суммы издержек обращения по ряду магазинов (в тыс. руб.). Данные представлены таблицей 1.

Таблица 1.

Из таблицы видно, что с ростом товарооборота растут и издержки обращения. График еще раз это подтверждает.

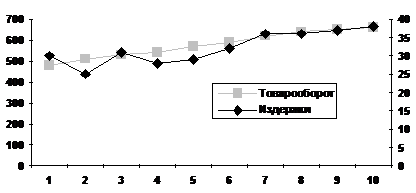
Но в ряде случаев увеличение товарооборота ведет и к уменьшению издержек обращения, поскольку, помимо двух названных величин, в реальном процессе торговли участвуют и другие факторы, которые в рассмотрение не включены и носят случайный характер. Рассмотрим критерий тесноты связи, названный показателем корреляции рангов. От величин абсолютных перейдем к рангам по такому правилу: самое меньшее значение — ранг 1, затем 2 и т. д. Если встречаются одинаковые значения, то каждое из них заменяется средним. Итак:

Построим разности между рангами и возведем их в квадрат.

Из за большого объема этот материал размещен на нескольких страницах: 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49