,

где - общая дисперсия;

- средняя из внутригрупповых дисперсий;

- межгрупповая дисперсия.

Таким образом, общая дисперсия складывается из двух слагаемых: первое – измеряет вариацию внутри частей совокупности, а второе – вариацию между средними этих частей.

Средняя из внутригрупповых дисперсий:

,

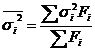где – групповые дисперсии; - число единиц в группах.

Межгрупповая дисперсия:

,

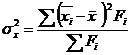где – групповые средние; - общая средняя.

1.5.5. Показатели дифферециации

Правило сложения дисперсий позволяет выявить зависимость результатов от определяющих факторов с помощью соотношения межгрупповой и общей дисперсий. Это соотношение называется коэффициентом детерминации и показывает, какая доля в общей дисперсии приходится на дисперсию, обусловленную вариацией признака, положенного в основу группировки.

Эмпирический коэффициент детерминации вычисляется по формуле:

.

Используется правило сложения дисперсий и для определения степени связи между изучаемыми признаками. Для этого необходимо найти эмприческое корреляционное отношение, которое показывает, насколько тесно связаны исследуемое явление и группировочный признак (чем ближе значение эмпирического корреляционного отношения к единице, тем теснее связь).

Эмпирическое корреляционное отношение определяется по формуле:

.

Под выборочным понимается метод статистического исследования, при котором обобщающие показатели изучаемой совокупности устанавливаются по некоторой ее части на основе положений случайного отбора. При выборочном методе обследованию подвергается сравнительно небольшая часть всей изучаемой совокупности (обычно до 5 - 10%, реже до 15 - 25%). При этом подлежащая изучению статистическая совокупность, из которой производится отбор части единиц, называется генеральной совокупностью. Отобранная из генеральной совокупности некоторая часть единиц, подвергающаяся обследованию, называется выборочной совокупностью или просто выборкой.

Значение выборочного метода состоит в том, что при минимальной численности обследуемых единиц проведение исследования осуществляется в более короткие сроки и с минимальными затратами труда и средств. Это повышает оперативность статистической информации, уменьшает ошибки регистрации.

В проведении ряда исследований выборочный метод является единственно возможным, например, при контроле качества продукции (товара), если проверка сопровождается уничтожением или разложением на составные части обследуемых образцов (определение сахаристости фруктов, клейковины печеного хлеба, установление носкости обуви, прочности тканей на разрыв и т. д.).

Проведение исследования социально-экономических явлений выборочным методом складывается из ряда последовательных этапов:

1) обоснование (в соответствии с задачами исследования) целесообразности применения выборочного метода;

2) составление программы проведения статистического исследования выборочным методом;

3) решение организационных вопросов сбора и обработки исходной информации;

4) установление доли выборки, т. е. части подлежащих обследованию единиц генеральной совокупности;

5) обоснование способов формирования выборочной совокупности;

6) осуществление отбора единиц из генеральной совокупности для их обследования;

7) фиксация в отобранных единицах (пробах) изучаемых признаков;

8) статистическая обработка полученной в выборке информации с определением обобщающих характеристик изучаемых признаков;

9) определение количественной оценки ошибки выборки;

10) распространение обобщающих выборочных характеристик на генеральную совокупность.

В генеральной совокупности доля единиц, обладающих изучаемым признаком, называется генеральной долей (обозначается р), а средняя величина изучаемого варьирующего признака — генеральной средней (обозначается ).

В выборочной совокупности долю изучаемого признака называют выборочной долей, или частостью (обозначается ), а среднюю величину в выборке — выборочной средней (обозначается ).

Пример. При контрольной проверке качества хлебобулочных изделий проведено 5%-ное выборочное обследование партии нарезных батонов из муки высшего сорта. При этом из 100 отобранных в выборку батонов 90 шт. соответствовали требованиям стандарта. Средний вес одного батона в выборке составлял 500,5 г при среднем квадратическом отклонении г.

На основе полученных в выборке данных нужно установить возможные значения доли стандартных изделий и среднего веса одного изделия во всей партии.

Прежде всего, устанавливаются характеристики выборочной совокупности. Выборочная доля, или частость, определяется из отношения единиц, обладающих изучаемым признаком m, к общей численности единиц выборочной совокупности n:

.

Поскольку из 100 изделий, попавших в выборку n, 90 ед. оказались стандартными m, то показатель частости равен: = 90:100=0,9.

Средний вес изделия в выборке = 500,5 г определен взвешиванием. Но полученные показатели частости (0,9) и средней величины (500,5 г) характеризуют долю стандартной продукции и средний вес одного изделия лишь в выборке. Дляопределения соответствующих показателей для всей партии товара надо установить возможные при этом значения ошибки выборки.

1.6.2. Средняя и предельная ошибка выборочного наблюдения для показателей средней и для доли

Ошибка выборки - это объективно возникающее расхождение между характеристиками выборки и генеральной совокупности. Она зависит от ряда факторов: степени вариации изучаемого признака, численности выборки, метода отбора единиц в выборочную совокупность, принятого уровня достоверности результата исследования.

Определение ошибки выборочной средней.

При случайном повторном отборе средняя ошибка выборочной средней рассчитывается по формуле:

,

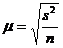где — средняя ошибка выборочной средней;

— дисперсия выборочной совокупности;

n — численность выборки.

При бесповторном отборе она рассчитывается по формуле:

,

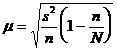где N — численность генеральной совокупности.

Определение ошибки выборочной доли.

При повторном отборе средняя ошибка выборочной доли рассчитывается по формуле:

,

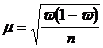где — выборочная доля единиц, обладающих изучаемым признаком;

— число единиц, обладающих изучаемым признаком;

— численность выборки.

При бесповторном способе отбора средняя ошибка выборочной доли определяется по формулам:

.

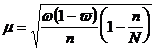Предельная ошибка выборки связана со средней ошибкой выборки отношением:

Из за большого объема этот материал размещен на нескольких страницах: 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49