Статистика (стр. 22 )

Например, в индексе цен индексируемой величиной служит цена, а весом - количество реализумой продукции (товаров).

Jp =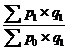

В этой формуле через “р” обозначаются цены, а через “q” - количество продукции (товаров).Подстрочные значки “0” и “1” обозначают соответственно текущий и базисный периоды.

Агрегатные индексы качественных показателей могут быть рассчитаны как индексы переменного и постоянного (фиксированного) состава. В индексах переменного состава сопоставляются показатели, рассчитанные на базе изменяющихся структур явлений, а в индексах постоянного состава - на базе неизменной структуры явлений.

Индекс переменного состава - показатель, представляющий отношение средних уровней изучаемого явления. Для получения индекса переменного состава необходимо рассчитать среднюю величину качественного показателя для каждого периода и затем найти отношение этих средних. Таким образом, индекс переменного состава является индексом среднего уровня явления. Например, индекс переменного состава производительности труда равен отношению:

Iw = : ,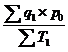

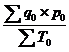где р0 - неизменные цены, q1 и q0 - количество продукции, произведенной соответственно в отчетном и базисном периодах, Т 1 и Т0- затраты труда, которые представляют собой произведение трудоемкости единицы продукции и количества произведенной продукции (tq).

На величине индекса переменного состава отражается не только изменение уровня изучаемого явления, но также изменение удельных весов элементов с различным уровнем этого явления во всей совокупности, то есть изменение состава.

Индекс постоянного (фиксированного) состава - это индекс качественного показателя (цены, себестоимости, производительности труда), рассчитанный для соизмеримой продукции (товаров), производимой (или реализуемой) различными предприятиями, в котором удельный вес предприятий фиксируется на уровне какого-либо одного периода. Индекс постоянного состава исчисляется как обычный сводный индекс.

Например, индекс постоянного состава производительности труда рассчитывается по формуле:

Iw =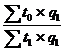

где t 0 и t1 - затраты труда на единицу продукции в базисном и текущем периодах.

Средние индексы - это средняя величина из индивидуальных индексов. В статистике рассчитываются взвешенные средние арифметические и средние гармонические индексы. Термином “средний индекс” иногда называют сводный индекс, так как он характеризует в среднем изменение элементов, составляющих сложное экономическое явление. Средний индекс всегда тождественен агрегатному индексу.

Средний арифметический индекс представляет собой среднюю арифметическую из индивидуальных индексов. Простая средняя арифметическая из индивидуальных индексов ( i : n) на практике не применяется, так как в ней не отражается удельный вес каждого отдельного элемента во всей совокупности. Средний арифметический индекс рассчитывается только как взвешенная величина.

Формула арифметического индекса получается путем замены значения индексируемой величины в числителе агрегатного индекса на равное ему произведение индивидуального индекса на значение индексируемой величины другого периода. Например, заменив в числителе агрегатного индекса физического объёма продукции количество продукции текущего периода q1 произведением iq q0 (где iq=q1:q0), получим средний арифметический индекс физического объёма продукции.

Iq =.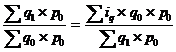

Это - средняя арифметическая из индивидуальных индексов объёма продукции (iq ), взвешенная по стоимости продукции базисного периода в базисных или сопоставимых ценах (p0).

Средний гармонический индекс представляет собой среднюю гармоническую из индивидуальных индексов. На практике средний гармонический индекс рассчитывается только как взвешенная величина. Для получения формулы данного индекса индексируемая величина, находящаяся в знаменателе агрегатного индекса, заменяется через индивидуальный индекс и индексируемую величину другого периода. Например, для построения среднего гармонического индекса цен заменяют в агрегатном индексе цену базисного периода (р0) равным ей отношением р1: i p.

Ip =.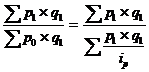

Этот индекс является средней гармонической из индивидуальных индексов цен (ip), взвешенной по величине товарооборота текущего периода (p1 q1).

При построении средних индексов следует руководствоваться следующим правилом: для индекса количественного показателя используют формулу среднего арифметического индекса, а для индекса качественного показателя - среднего гармонического индекса.

Средние индексы рассчитываются в тех случаях, когда нет необходимой информации для расчета агрегатного индекса.

При вычислении индексов различают сравниваемый уровень (текущий, отчетный) и уровень, с которым производится сравнение (базисный). Выбор базы сравнения определяется целью исследования. В индексах, характеризующих изменение индексируемой величины во времени, за базисную величину принимают размер явления в каком-либо периоде, предшествующем отчетному. При этом возможны два способа расчета индексов - цепной и базисный. Цепные индексы получают сопоставлением индексируемой величины последующего периода с показателем предшествующего ему периода. В этом случае база сравнения непрерывно меняется. Базисные индексы получают сопоставлением индексируемого показателя каждого периода с соответствующим показателем какого-то одного определенного периода, принятого за базу сравнения.

Индексы предназначены для решения следующих основных задач: характеристика изменения сложного социально-экономического явления во времени, пространстве или по сравнению с запланированными показателями; измерение значений отдельных факторов, их влияния на общее изменение изучаемого явления в динамике.

1.9.2. Индексы количественных показателей

Как уже отмечалось выше, необходимость построения индексов количественных показателей возникает в том случае, когда итоги по отдельным элементам сложного явления непосредственно несоизмеримы. Например, предприятие выпускает продукцию различного вида. Если имеются данные о выпуске продукции только в натуральном выражении, то динамику выпуска продукции в целом нельзя охарактеризовать отношением q1 : q0 , где q0 и q1 - количество продукции данного вида, выпущенной в базисном и отчетном периоде. Для получения общего итога необходимо данные по различным видам продукции привести к единой, общей мере, например, использовать стоимостную оценку продукции. Тогда вместо получим , где р - цена единицы продукции данного вида.

Выбор коэффициента соизмерения в каждом конкретном случае зависит от имеющейся исходной информации и от цели исследования. Универсальное значение в индексах физического объёма имеют стоимостные соизмерители. Умножая цену (себестоимость) на количество выпущенной продукции и суммируя произведения, получаем объём выпущенной продукции, который можно обозначить следующим образом:

в базисном периоде - или ,

в отчетном периоде - или ,

где i= 1, 2, 3,....n - число отдельных видов продукции.

При построении индексов объёмных показателей следует руководствоваться следующим правилом: в качестве соизмерителя применяются те или иные качественные показатели (чаще всего - цена, себестоимость), зафиксированные как правило на уровне базисного периода. Для измерения роста (снижения) изучаемых показателей в динамике применяют цены (себестоимость) одного и того же периода.

Если разделить стоимость продукции (работ, услуг) отчетного периода (p1q1 ) на стоимость продукции (работ, услуг) базисного периода (p0q0), то получим индекс стоимости продукции (работ, услуг): Ipq =.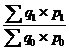

Этот индекс характеризует изменение стоимости продукции (работ, услуг), которая зависит от изменения уровня цен и объёма произведенной продукции (выполненных работ, оказанных услуг) в отчетном периоде по сравнению с базисным. Индекс стоимости не дает количественного представления об изменении объёма выпущенной продукции (выполненных работ, оказанных услуг). Такое представление можно получить рассчитав влияние изменения цен, для чего количество продукции, произведенной в отчетном и базисном периоде, надо умножить на одинаковые для обоих периодов цены: Iq = .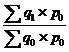

Такой индекс называют агрегатным индексом физического объёма. В числителе и знаменателе изменяется индексируемая величина (q), а значение соизмерителя (p) остается неизменным.

Рассмотрим пример расчета индивидуальных и агрегатных индексов физического объёма продукции.

Индивидуальные индексы физического объёма продукции можно вычислить по следующей формуле: iq = q 1 : q0 .

Из за большого объема этот материал размещен на нескольких страницах: 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49