Статистика (стр. 25 )

Для того, чтобы измерить влияние изменений в структуре весов на показатель изменения уровня себестоимости продукции следует рассчитать отношение средних взвешенных с одними и теми же весами, то есть исчислить индекс постоянного состава.

Формула индекса средней себестоимости продукции постоянного состава выглядит следующим образом:

.

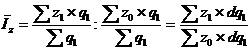Средняя себестоимость продукции в базисном периоде скорректирована на структуру фактического выпуска продукции. Следовательно, данное отношение показывает каково было бы изменение среднего уровня себестоимости продукции по группе предприятий, если бы удельный вес предприятий с разным уровнем себестоимости в базисном периоде был таким же, как и в отчетном.

Как уже отмечалось выше, величина взвешенной средней зависит от двух факторов: изменения отдельных уровней индексируемой величины (значение “ z” на отдельных предприятиях) и от изменения в структуре весов. Поэтому, если веса не остаются постоянными, то индекс фиксированного состава будет отличаться от индекса переменного состава в меру отношения:

Id==.

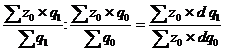Указанное отношение принято называть индексом влияния структурных сдвигов, который представляет собой отношение среднего уровня себестоимости продукции базисного периода, скорректированного на отчетную структуру производства определенного вида продукции, и фактической средней себестоимости продукции базисного периода.

Рассмотрим на примере расчет индексов себестоимости продукции переменного, постоянного состава и структурных сдвигов.

Для оценки снижения уровня себестоимости единицы продукции по двум предприятиям в целом рассчитаем средние уровни себестоимости единицы продукции:

= 11024 : 9200 = 1,20 млн. рублей

= 13212 : 11240 = 1,18 млн. рублей

Далее, вычислим индекс себестоимости продукции переменного состава: = 1 : 0 = 1,18 : 1,20 = 0,983

Средняя себестоимость единицы продукции по двум предприятиям в отчетном году по сравнению с базисным годом снизилась на 1,7 %.

Изменение средней себестоимости единицы продукции за счет изменения уровня себестоимости продукции на каждом предприятии оценивается индексом себестоимости продукции постоянного состава:

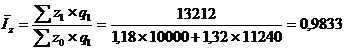
В среднем уровень себестоимости продукции снизился на каждом предприятии в отчетном периоде по сравнению с базисным на 1,67 %.

C помощью индекса влияния структурных сдвигов можно определить снижение средней себестоимости единицы продукции за счет перемещения объемов производства продукции на предприятие с более низкой себестоимостью:

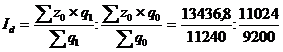= 0,9975

За счет изменения в соотношении выпуска продукции между предприятиями средняя себестоимость продукции снизилась в отчетном периоде по сравнению с базисным на 0,25 %.

Взаимосвязь индексов переменного, постоянного состава и структурных сдвигов можно описать следующим равенством:

Iz = IzId 0,98 = 0,9833 0,9975

В отдельных случаях могут быть известны не абсолютные значения индексируемых показателей, а их относительные изменения. В такой ситуации агрегатный индекс можно рассчитать косвенным путем, используя взвешенную среднюю из индивидуальных индексов, если нам известен размер результативной величины за отчетный период. Рассмотрим на примере расчет среднего гармонического индекса себестоимости продукции.

Общий индекс себестоимости продукции можно рассчитать по следующей формуле: Iz=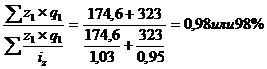

Исходя из того, что издержки производства представляют собой произведение количества выпущенной продукции (q) и себестоимости единицы продукции (z), мы можем построить следующую систему индексов:

Izq = Iq Iz

где Izq - индекс издержек производства, Iq - индекс физического объема продукции и Iz - индекс себестоимости единицы продукции.

На основе такой системы индексов мы можем рассчитать общее изменение издержек производства в отчетном периоде по сравнению с базисным, а также изменение издержек производства за счет отдельных факторов в абсолютном и относительном выражении по приведенной ниже схеме.

1. Определим общее изменение издержек производства:

- относительное изменение вычислим с помощью индекса издержек производства

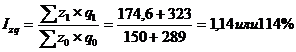I

- абсолютное изменение рассчитаем как разность между числителем и знаменателем индекса издержек производства

zq = z 1 q1 - z0 q0 = 58,6 млн. рублей.

2. Определим изменение издержек производства за счет отдельных факторов:

а) за счет изменения себестоимости единицы продукции

- относительное изменение вычислим с помощью индекса себестоимости продукции Iz = 0,98 или 98 %

- абсолютное изменение рассчитаем как разность между числителем и знаменателем индекса себестоимости продукции

zqz = z 1 q1 - z0 q1 = 497,6-509,5=-11,9 млн. рублей.

б) за счет изменения количества выпущенной продукции

- относительное изменение вычислим с помощью индекса физического объема продукции

Iq = Izq : Iz = 1,14 : 0,98 = 1,16 или 116 %

- абсолютное изменение рассчитаем исходя из взаимосвязи исчисленных показателей

zq q = zq - zqz = 58,6 + 11,9 = 70,5 млн. рублей

Таким образом, издержки производства в отчетном периоде по сравнению с базисным возросли на 14 % или 58,6 млн. рублей в результате увеличения производства продукции на 16 % или 70,5 млн. рублей при общем снижении себестоимости единицы продукции на 2 % или 11,9 млн. рублей.

В рыночной экономике особое место среди индексов качественных показателей отводится индексам цен. С помощью индекса цен можно оценить динамику цен на товары (работы, услуги) и измерить уровень инфляции.

Автором первой формулы агрегатного индекса цен является немецкий статистик Г. Пааше:

Ip = .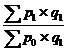

Немецкий ученый Э. Ласпейрес предложил определять индекс цен следующим образом:

Ip = .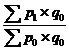

Индексируемой величиной обоих индексов являются цены. Весами в индексе цен Пааше выступает количество продукции текущего периода, а в индексе цен Ласпейреса - количество продукции базисного периода. Значение индексов цен Пааше и Ласпейреса не совпадают, так как индексы имеют различное экономическое содержание. Индекс цен Пааше показывает насколько товары (работы, услуги) в отчетном периоде стали дороже (дешевле), чем в базисном. Индекс цен Ласпейреса дает ответ на вопрос во сколько бы раз товары (работы, услуги) базисного периода подорожали (подешевели) из-за изменения цен на них в отчетном периоде. Согласно практике индекс цен, рассчитанный по формуле Пааше, имеет тенденцию некоторого занижения, а по формуле Ласпейреса - завышения темпов инфляции.

Из за большого объема этот материал размещен на нескольких страницах: 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49