1. Если ранги совпадают, то ясно, что сумма их квадратов равна 0.
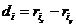
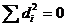
Связь полная, прямая.
2. Ранги образуют обратную последовательность
1 10
2 9 В этом случае ![]()
3 8
. . Связь полная, обратная.
. .
. .
10 1
3. Среднее значение из двух крайних означает полное отсутствие связи:
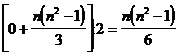
4. Показатель корреляции рангов:
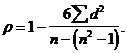
Показатель показывает, как отличается полученная при наблюдении сумма квадратов разностей между рангами от случая отсутствия связи.
Проанализируем показатель корреляции рангов.
1. Связь полная и прямая, 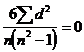 и
и ![]()
2. Связь полная и обратная, 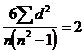 и
и ![]()
3. Все остальные значения лежат между -1 и +1.
Построим показатель корреляции рангов для нашего примера:
Товарооборот (ранг) | Издержки (ранг) |
|
|
1 | 4 | -3 | 9 |
2 | 1 | 1 | 1 |
3 | 5 | -2 | 4 |
4 | 2 | 2 | 4 |
5 | 3 | 2 | 4 |
6 | 6 | 0 | 0 |
7 | 7,5 | -0,5 | 0,25 |
8 | 7,5 | 0,5 | 0,25 |
9 | 9 | 0 | 0 |
10 | 10 | 0 | 0 |
|
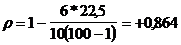
Полученный показатель свидетельствует о достаточно тесной связи между товарооборотом и издержками.
Для определения тесноты корреляционной связи применяется коэффициент корреляции.
Коэффициент корреляции изменяется от -1 до +1 и показывает тесноту и направление корреляционной связи.
Если отклонения по ![]() и по
и по ![]() от среднего совпадают и по знаку, и по величине, то это полная прямая связь, то
от среднего совпадают и по знаку, и по величине, то это полная прямая связь, то ![]() =+1.
=+1.
Если полная обратная связь, то ![]() =-1.
=-1.
Если связь отсутствует, то ![]() =0.
=0.
Наиболее удобной формулой для расчета коэффициента корреляции является:
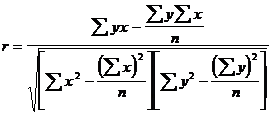 (1)
(1)
Коэффициент корреляции можно рассчитать и по другой формуле:
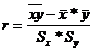 , (2)
, (2)
где
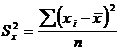 и
и 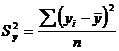
Пример.
Вернемся к примеру, где были рассмотрены товарооборот и издержки обращения по 10 магазинам.
Таблица
Товаро- борот(х) | Издержки обращения (у) |
|
|
|
480 | 30 | 230400 | 900 | 14400 |
510 | 25 | 260100 | 625 | 12750 |
530 | 31 | 280900 | 961 | 16430 |
540 | 28 | 291600 | 784 | 15120 |
570 | 29 | 324900 | 841 | 16530 |
590 | 32 | 348100 | 1024 | 18880 |
620 | 36 | 384400 | 1296 | 22320 |
640 | 36 | 409600 | 1296 | 23040 |
650 | 37 | 422500 | 1369 | 24050 |
660 | 38 | 435600 | 1444 | 25080 |
|
|
|
|
|
Все необходимые данные для определения коэффициента корреляции есть в таблице, их лишь остается подставить в необходимую формулу.
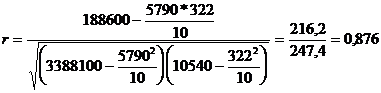
В ряде случаев возникает необходимость установления статистической связи между признаками, не имеющими количественного выражения.
Пример.
На предприятии работает группа станков. В силу организационно-технических причин, периодически возникают простои. Было проведено 133 наблюдения за работой станков на протяжении дня, при этом в 59 случаях были отмечены простои, соответственно в 74 случаях их не было. После рационализаторского предложения, направленного на уменьшение простоев, вновь было проведено наблюдение, но уже за 66 станками. При этом в 27 случаях были отмечены простои, в 39 — нет. Ставиться вопрос: а есть ли вообще связь между сделанным предложением и уменьшением простоев. либо это вообще между собой никак не соотносится.
В данном случае сопоставляются два признака, причем альтернативных.
1 признак — наличие или отсутствие рационального предложения;
2 признак — наличие или отсутствие простоев.
Ни тот, ни другой признак нельзя выразить числено. Поэтому введем следующие обозначения.
Первый признак (х): — наличие рационального предложения (1), отсутствие — (0).
Второй признак (у): — отсутствие простоев (1), наличие простоев (0).
Наши наблюдения представим таблицей:
66 | 133 | 199 | |
0 | 27 | 74 | 101 |
1 | 39 | 59 | 98 |
x | 1 | 0 |
Для центральной части таблицы введем специальные обозначения
c | d |
a | b |
В этих обозначениях коэффициент корреляции имеет вид:
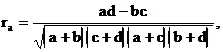
его еще называют коэффициентом ассоциации.
Он так же меняется от -1 до +1 и для нашего примера равен:
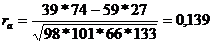
Очень маленький коэффициент. Показывает, что связь между рациональным предложением и уменьшением числа простоев очень мала. Конечно, простои уменьшились, но не на столько эффективно, как бы этого хотелось.
1.8. Ряды динамики и их применение в анализе социально-экономических явлений
1.8.1. Установление вида ряда динамики
Основная цель статистического изучения динамики экономических процессов состоит в выявлении и измерении закономерностей их развития во времени. Это достигается посредством построения и анализа статистических рядов динамики.
Рядами динамики называются статистические данные, отображающие развитие изучаемого явления во времени. В каждом ряду динамики имеются два основных элемента: показатель времени t; соответствующие им уровни развития изучаемого явления у. В качестве показаний времени в рядах динамики выступают либо определенные даты (моменты) времени, либо отдельные периоды (годы, кварталы, месяцы, сутки).
Уровни рядов динамики отображают количественную оценку (меру) развития во времени изучаемого явления. Они могут выражаться абсолютными, относительными или средними величинами.

|
Из за большого объема этот материал размещен на нескольких страницах:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 |



