Министерство образования Российской Федерации

Владивостокский государственный университет

экономики и сервиса

___________________________________________

Е. Ф. ЧУБЕНКО

Г. Л. ОВСЯННИКОВА

ТЕОРЕТИЧЕСКАЯ МЕХАНИКА

Часть 1

Учебное пособие

Владивосток

Издательство ВГУЭС

2003

ББК 22.21

Ч 81

Рецензент , канд. техн. наук, профессор каф. ФХ и ПМ ВГУЭС

,

Ч 81 ТЕОРЕТИЧЕСКАЯ МЕХАНИКА: Учебное посо­бие. Ч. 1. – Вла­дивосток: Изд-во ВГУЭС, 2003 – 128с.

Учебное пособие представляет собой комплекс, содержа­щий основные сведения о теории, необходимые для самостоя­тельного решения задач. В каждом разделе даны рекомендации о последовательности решения различных типов задач и приведены подробные методические указания к решению подобных задач. Может использоваться как теоретическая часть при подготовке к сдаче экзамена или зачета, так и в качестве методических указа­ний к решению задач на практических занятиях, при выполнении контрольных работ заочниками и расчётно-графических заданий.

Для студентов всех форм обучения.

ББК 22.21

ã Издательство Владивостокского

государственного университета

экономики и сервиса, 2003

Глава 1. ПЛОСКАЯ СИСТЕМА СХОДЯЩИХСЯ СИЛ

§ 1. Сложение двух сходящихся сил

Если в одной точке к телу приложены две силы под углом друг к другу, то их сложение выполняется по правилу параллело­грамма.

Модуль равнодействующей R может быть определен аналитиче­ски из треугольника АВС с помощью теоремы косинусов (рис. 1):

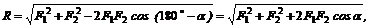
так как .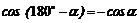

Направление равнодействующей определяется углами и , которые можно рассчитать, применив теорему синусов. Для тре­угольника ABC

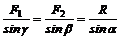, (1)

откуда, учитывая, что 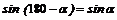, получим

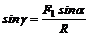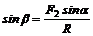, . (2)

Вместо параллелограмма сил можно строить силовой треугольник (рис. 2). Выбрав любую точку на плоскости рисунка, проводят из нее, сохраняя масштаб, вектор, равный и параллельный одной из заданных сил, например F1.

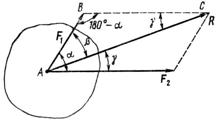
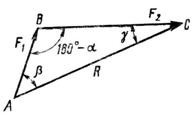
Рис. 1 Рис. 2

Из конца вектора F1 проводят вектор, равный и параллельный второй силе, F2. Начало первого вектора соединяют с концом второго, замыкая треугольник. Замыкающая сторона треуголь­ника в данном масштабе представляет собой искомую равнодей­ствующую. Модуль и направление равнодействующей определяют аналитически, как было показано выше.

При построении треугольника сил необходимо придерживаться правила: стрелки составляющих векторов направлены в одну сторону, а равнодействующей – им навстречу.

Частные случаи: 1) если , т. е. силы действуют по одной прямой в одну строну, то

;

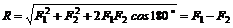2) если , т. е. силы действуют по одной прямой в разные стороны, то

;

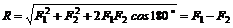3) если , то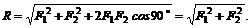

Заметим, что определение равнодействующей двух сил по правилу параллелограмма или треугольника называется вектор­ным, или геометрическим, сложением.

Задача 1. Определить равнодействующую двух сил и , модули которых соответственно равны Р1 = 40 Н и Р2 = 80 Н; сила направлена горизонтально вправо, а образует с угол a = 120° (рис. 3, а).

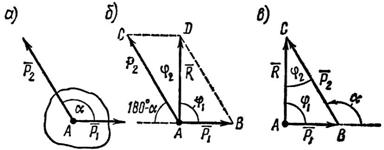
Рис. 3

Задачу можно решить графоаналитическим методом, используя либо правило параллелограмма, либо правило треугольника.

Решение 1 – по правилу параллелограмма:

1. Используя условие задачи и приблизительно соблюдая мас­штаб, изображаем параллелограмм ABCD (рис. 3, б). Порядок построения такой: из точки А проводим отрезок , затем из той же точки А под углом 120° к отрезку АВ проводим отрезок , из точек В и С проводим прямые BD || АС и CD || AB и, наконец, проводим диагональ

2. Используя формулу (1), можем найти модуль равнодействующей:

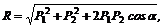
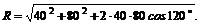
Имея в виду, что cos120° = – sin 30° = – 0,5, получаем

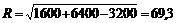Н.

3. Применяя к D ABD (или к D ACD) (см. рис. 3, б) теорему синусов, получаем

,

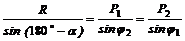откуда

и ,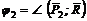

;

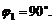
Таким образом, вектор равнодействующей перпендикулярен к силе ,

Угол j2 можно найти либо как разность

либо из теоремы синусов:

и j2 = 30°.

Один и тот же результат, полученный различными путями, под­тверждает правильность решения задачи.

Ответ. Равнодействующая данных сил равна 69,3 Н и линия ее действия образует с направлением силы прямой угол.

Решение 2 – по правилу треугольника.

1. Используя условие задачи, строим треугольник сил ABC (рис. 3, в). Порядок построения такой: из точки А проведем отре­зок . Затем из точки В под углом a = 120° к направлению проводим отрезок и, наконец, «замкнем» треугольник отрезком АС, который изобразит искомую равнодействующую

В получившемся треугольнике

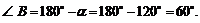
2. Применяем к треугольнику ABC известную из тригонометрии теорему косинусов:

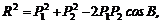
откуда модуль равнодействующей

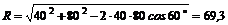Н.

3. Углы j1 и j2, определяющие направление равнодействующей относительно заданных сил, находим, как и в первом решении, по теореме синусов.

§ 2. Разложение силы на две сходящиеся составляющие

Любую силу можно рассмотреть как равнодействующую двух произвольных, сходящихся под углом сил. Модуль и направление составляющих сил зависят от угла между ними. Можно построить множество параллелограммов, для которых данная сила R будет служить диагональю (рис. 4). Чтобы задача стала определенной, нужно знать одно из дополнительных условий: модули обеих составляющих, модуль и направление одной из составляющих, направление обеих составляющих, модуль одной из составляющих и направление другой.

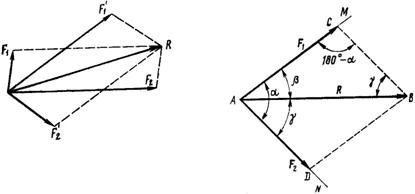
Рис. 4 Рис. 5

Каждую из задач можно решить двумя способами: графическим и графоаналитическим.

При графическом решении задачи заданную силу откладывают на чертеже в выбранном масштабе, а затем производят несложные геометрические построения в зависимости от заданных условий.

Для графоаналитического решения нет надобности соблюдать масштаб, но при построении нужно сохранять примерное напра­вление сил. Модули составляющих сил либо углы, определяющие их направление, вычисляют, пользуясь формулами (1) и (2).

Например, если заданы только направления составляющих сил, то из точки А вектора R (рис. 5) проводим линии действия со­ставляющих AM и AN под известными углами и Затем из точки В проводим прямые, параллельные этим линиям, т. е. строим параллелограмм, в котором стороны АС и AD предста­вляют собой искомые силы F1 и F2 в данном масштабе.

Из за большого объема этот материал размещен на нескольких страницах: 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20