2. Освободив вал в точках A и B от опор, заменяем действие опор их реакциями: подшипник А не препятствует горизонтальному смещению вала, поэтому его реакцию, расположенную в плоскости, перпендикулярной к оси вала, заменяем двумя составляющими: горизонтальной и вертикальной подпятник В препятствует смещению вала вдоль его оси, поэтому его реакцию заменяем тремя составляющими и (см. рис. 59, б).
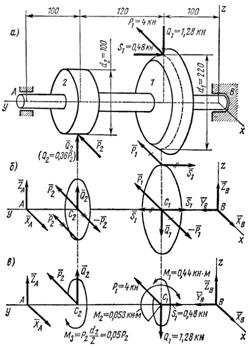
Рис. 59
3. Если силы выражать в кH, а плечи пар в м, то получим такие абсолютные числовые значения моментов М1 и М2:
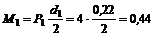 кН×м;
кН×м;
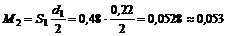 кН×м;
кН×м;
а момент М3 выразится так:
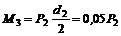 .
.
4. Составим шесть уравнений равновесия.
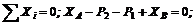 (1)
(1)
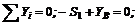 (2)
(2)
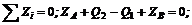 (3)
(3)
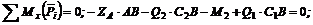 (4)
(4)
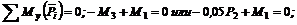 (5)
(5)
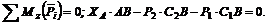 (6)
(6)
5. Решая эти уравнения последовательно, получим: из уравнения (5)
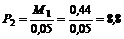 кН.
кН.
Так как
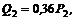
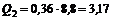 кН.
кН.
Из уравнения (6)
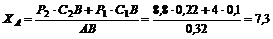 кН.
кН.
Из уравнения (4)
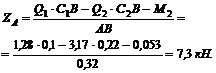
Реакция ZА направлена не вверх, как на рис. 177, в, а вниз. Из уравнения (3)
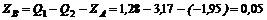 кН.
кН.
Из уравнения (2) 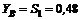 кН.
кН.
Из уравнения (1) 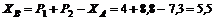 кН.
кН.
Глава 4. КИНЕМАТИКА ТОЧКИ
§ 14. Основные положения кинематики
Кинематика – это часть теоретической механики, которая занимается изучением законов механического движения твердых тел. Под механическим движением понимают перемещение тел в пространстве, совершаемое во времени. При изучении движения тел в кинематике не принимаются во внимание силы, действующие на тела, а также физические свойства самих тел.
О наличии движения и его характере можно судить по изменению положения данного тела по отношению к некоторой системе координат, которые чаще всего связывают с Землей как системой отсчета.
Известно, что при изучении некоторых случаев движения можно пренебречь размерами и формой тела, рассматривая его как материальную точку. Так, например, при поступательном движении все точки тела движутся одинаково, поэтому такое тело можно рассматривать как материальную точку, в которой сосредоточена вся масса тела.
В других случаях движения, например вращательном, все точки тела движутся по-разному. При этом твердое тело рассматривают как неизменяемую систему материальных точек. Поэтому кинематика делится на две части: кинематику точки и кинематику твердого тела.
Движение тела является заданным, если известно, как изменяется его положение в пространстве относительно выбранной системы координатных осей с течением времени.
Положение тела в пространстве в данный момент времени определяется его координатами, т. е. расстояниями от этих осей.
Для измерения расстояний в системе СИ принята основная единица – метр (м).
Для измерения времени принята основная единица – секунда (с).
Причем в кинематике различают такие понятия, как момент времени и промежуток времени.
Моментом времени t считают число секунд, определяющее данное мгновенье от некоторого, условно принятого начального момента (начала движения).
Промежутком времени называют разность между более поздним и ранним моментом времени. Например, автомобиль в некоторый момент времени t1 находился в пункте A, а позже, в момент t2, переместился в пункт В. Перемещение автомобиля из пункта А в пункт В произошло за промежуток времени D t = t2 – t1. Воображаемую линию, описываемую определенной точкой движущегося тела, называют траекторией движения. В зависимости от формы траектории движение может быть криволинейным или прямолинейным.
Величину, характеризующую быстроту и направление движения тела по траектории с течением времени, называют скоростью движения. Скорость – величина векторная.
В общем случае, если модуль и направление вектора скорости с течением времени изменяются, то движение является неравномерным и криволинейным. Если модуль и направление вектора скорости не изменяются с течением времени, то движение будет равномерным и прямолинейным.
Возможны и другие частные случаи движения, при которых переменны либо модуль, либо направление вектора скорости. За единицу модуля скорости принимают м/с. Быстроту изменения модуля и направления скорости по времени называют ускорением движения. Ускорение, как и скорость, является векторной величиной. Единицей измерения ускорения является м/с2.
§ 15. Способы задания движения точки
Движение точки можно задать двумя способами.
1. Координатный способ. Этот способ основан на том, что положение любой точки М в пространстве определяется тремя координатами относительно выбранной неподвижной системы трех взаимно перпендикулярных осей (рис. 60). При движении точки ее координаты являются функциями времени, т. е.
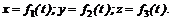
Данные уравнения называют уравнениями криволинейного движения точки в прямоугольных координатах. Если точка движется все время в одной плоскости, то уравнений будет только два:
x = f1(t); у = f1(t).
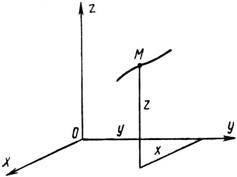
Рис. 60
Если же точка совершает прямолинейное движение, то, направив одну из осей, например ось х, по направлению движения точки, получим одно уравнение х = f (t), которое полностью определит это движение.
Задавшись системой координат и зная уравнения движения, можно определить положение движущейся точки в любой момент времени.
2. Естественный способ. Этот способ основан на том, что положение точки М на траектории (рис. 61) определяется длиной дуги траектории s = ÈОМ. Каждому положению точки М соответствует свое значение s, т. е.
s = f(t) (21)
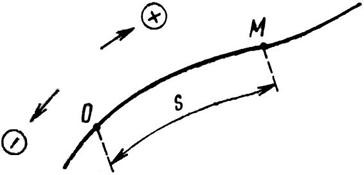
Рис. 61
Уравнение (21) выражает функциональную зависимость между расстоянием s точки от начала отсчета и временем движения. Его называют уравнением движения (законом движения) точки по данной траектории. Расстояние s, пройденное точкой от начала отсчета О, может быть положительным либо отрицательным в зависимости от направления движения точки. Таким образом, движение точки задано, если известны ее траектория и закон движения по этой траектории.
Следует различать два понятия: расстояние и путь, пройденный точкой. Если расстояние может быть как положительным, так и отрицательным, то путь, пройденный точкой, всегда является величиной положительной.
Действительно, пусть в некоторый момент времени t1 точка находится на траектории в положении М0 (рис. 62) на расстоянии S0 от начала отсчета 0. Двигаясь слева направо, точка в момент времени t2 оказалась в положении М1. Путь, пройденный точкой S, может быть определен как
S = S1 – S0.
Рис. 62
Таким образом, путь равен разности между конечным и начальным для рассматриваемого промежутка времени расстояниями. Очевидно, что при S0 = 0, S = S1, т. е. путь совпадает с расстоянием, если положение точки в начале рассматриваемого промежутка времени совпадало с принятым началом отсчета.
При изучении кинематики точки ограничимся только естественным способом задания движения. Начнем изучение с криволинейного движения, которое представляет собой общий случай движения.
§ 16. Скорость точки
Равномерное движение точки. Рассмотрим сначала равномерное движение точки М по траектории. Пусть в начале движения точка была в начале отсчета 0 и за t секунд прошла расстояние (путь) S. Равномерным движением называется такое движение, при котором отношение пройденного пути ко времени движения есть величина постоянная, т. е. S / t = const.
Это отношение называют скоростью равномерного движения точки. Модуль вектора скорости равен:
![]() (22)
(22)
Вектор скорости V направлен по касательной к траектории точки в сторону движения.
Из выражения (22) определим расстояние:
S = Vt (23)
и время движения:
![]() (24)
(24)
Данные уравнения являются основными формулами равномерного движения. Если в начале рассматриваемого промежутка времени точка находилась не в начале отсчета, а на некотором расстоянии S0 от него, то формула (23) примет вид
S = S0 + Vt,
где S0 – начальное расстояние; S – расстояние точки М от начала отсчета.
Задача 33. Из двух пунктов А и В прямолинейного шоссе, находящихся один от другого на расстоянии 100 км, одновременно выезжают навстречу друг другу два велосипедиста и двигаются с постоянными скоростями. Велосипедист, выезжающий из А, имеет скорость vА = 40 км/ч, а велосипедист, выезжающий из В – скорость VВ = 262/3 км/ч.

|
Из за большого объема этот материал размещен на нескольких страницах:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 |




