4. Расположим систему координатных осей, как показано на рис. 49, в, и составим три уравнения равновесия:
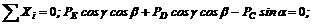 (1)
(1)
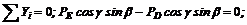 (2)
(2)
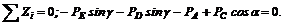 (3)
(3)
Замечая, что g = 45° (так как треугольники ВАЕ и BAD имеют равные катеты BA = AE =AD и a = b = 60°), решаем получившиеся уравнения.
Из уравнения (2) РЕ= PD.
Теперь уравнения (1) и (3) примут такой вид:
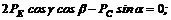 (4)
(4)
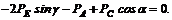 (5)
(5)
Умножим обе части уравнения (5) на cos b и сложим его после этого с уравнением (4):
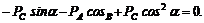
Отсюда
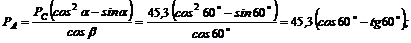 PA= – 55,8 кН.
PA= – 55,8 кН.
Знак «минус» указывает на то, что реакция направлена не от узла В, а к узлу, т. е. стойка сжата силой 55,8 кН.
Подставив найденное значение РА = – 55,8 кН в уравнение (5), найдем реакции РЕ и PD:
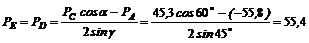 кН.
кН.
Тросы AD и AE растянуты усилиями по 55,4 кН.
§ 12. Момент силы относительно оси
Если к телу, имеющему ось вращения, приложить силу F, то она будет стремиться вращать тело вокруг этой оси. В этом случае действие силы на тело измеряется величиной момента силы относительно оси (рис. 50).
Момент силы относительно оси равен взятому со знаком «плюс» или «минус» произведению модуля проекции силы на плоскость, перпендикулярную этой оси (F'), на кратчайшее расстояние а (плечо) от этой проекции до точки пересечения оси с плоскостью:
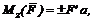
где F' = F cos a – модуль проекции силы F на плоскость (a – угол наклона линии действия силы к плоскости); а – плечо, следовательно:
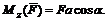 (18)
(18)
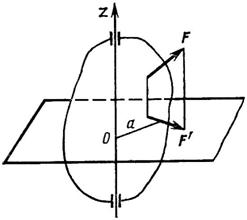
Рис. 50
Условимся считать момент положительным, если наблюдатель, смотрящий на плоскость со стороны положительного конца оси, видит возможное вращение плоскости по часовой стрелке. В противном случае – момент отрицательный. Из формулы (18) следует, что момент силы относительно оси равен нулю в двух случаях: если сила параллельна оси (сила F1 рис. 51), т. е. при a = 90° или 270°, когда cos a = 0, и если a = 0, т. е. линия действия силы пересекает ось (сила F2). Момент силы относительно оси будет наибольшим, если a = 0, т. е. сила лежит в плоскости, перпендикулярной оси (сила F3). Тогда Мz(F3) = F3a.
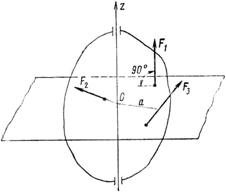
Рис. 51
Задача 28. К вершинам квадрата ABCD(AB = AD = 2 м), расположенного в горизонтальной плоскости, приложены силы , , и , как показано на рис. 52. Сила направлена по диагонали АС; сила действует вверх перпендикулярно к плоскости квадрата; сила действует в плоскости квадрата, и ее направление образует с диагональю СА угол a = 20°; сила действует в плоскости, перпендикулярной к плоскости квадрата, и направлена к стороне DC под углом b = 30°. Определить моменты каждой силы относительно осей х, у и z. Модули сил P1 = Р2 = Р3 = Р4 = 5 кН.
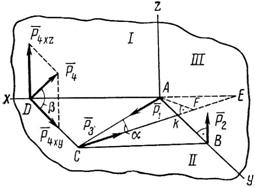
Рис. 52
Решение.
1. Замечаем, что расположение осей, показанное на рис. 52, определяет положение трех взаимно перпендикулярных плоскостей; плоскости I, перпендикулярной к оси у, плоскости II, перпендикулярной к оси z, и плоскости III, перпендикулярной к оси х.
2. Определяем моменты силы . Сила приложена в точке А пересечения всех трех осей, следовательно, согласно первому частному случаю,
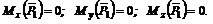
3. Определяем моменты силы .
Сила , приложенная в точке В, пересекает ось у и параллельна оси z. Следовательно, согласно первому и второму частным случаям
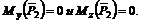
Чтобы определить момент силы относительно оси х, необходимо найти проекцию на плоскость III, перпендикулярную к оси х. Сила расположена в этой плоскости и, следовательно, проектируется полностью Р2yz = Р2. Плечом является сторона АВ квадрата. Знак момента положительный, так как если посмотреть от точки D вдоль оси х на плоскость III, то увидим, что сила поворачивает плечо АВ против хода часовой стрелки. Поэтому
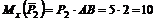 кН×м.
кН×м.
4. Определяем моменты силы ![]() .
.
Сила ![]() расположена в горизонтальной плоскости. В этой же плоскости расположены оси х и у. Поэтому линия действия силы
расположена в горизонтальной плоскости. В этой же плоскости расположены оси х и у. Поэтому линия действия силы ![]() пересекает ось х (в точке Е) и ось у (в точке К). Значит,
пересекает ось х (в точке Е) и ось у (в точке К). Значит,
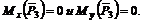
Плоскость, в которой расположена сила ![]() , перпендикулярна оси z, значит, Р3ху = Р3. Плечо AF силы
, перпендикулярна оси z, значит, Р3ху = Р3. Плечо AF силы ![]() найдем из треугольника AFC:
найдем из треугольника AFC:
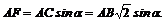
Знак момента положительный (если посмотреть на плоскость II со стороны оси z). Поэтому
 кН×м.
кН×м.
5. Определяем моменты силы ![]() . Линия действия силы
. Линия действия силы ![]() пересекает ось х, следовательно,
пересекает ось х, следовательно,
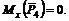
Спроектируем силы ![]() на плоскости I и II:
на плоскости I и II:
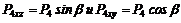 ;
;
плечом силы ![]() является сторона квадрата AD.
является сторона квадрата AD.
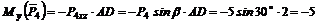 кН×м;
кН×м;
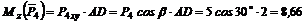 кН×м.
кН×м.
§ 13. Условия равновесия произвольной
пространственной системы сил
Пространственную систему произвольно расположенных сил, как и плоскую систему, можно привести к простейшему виду, т. е. к главному вектору и главному моменту. Для этого, выбрав центр приведения, переносим в него параллельно все силы системы, одновременно присоединяя соответствующие пары. В результате в центре приведения получим пространственную систему сходящихся сил и пространственную систему пар. Сложив все силы пучка, найдем главный вектор системы. Его значение можно определить по формуле
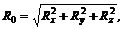
где 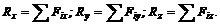
Складывая присоединенные пары, получим результирующую пару, момент которой называют главным моментом системы. Зная, что момент пары – вектор, разложим вектор главного момента по правилу параллелепипеда на три составляющие, направленные по трем взаимно перпендикулярным осям (рис. 53) Мx, Мy, и Мz. Тогда модуль главного момента можно определить по формуле
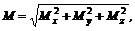
где Мх, My и Мz – проекции главного момента на оси.
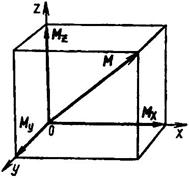
Рис. 53
Можно доказать, что проекции Мх, Му и Мz, каждая соответственно равна алгебраической сумме моментов всех сил данной системы относительно осей координат, т. е.
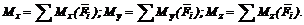
Чтобы пространственная система сил была в равновесии, необходимо соблюдение условий R0 = 0 и М = 0, т. е.
![]()
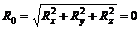 , и
, и 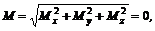
что соответствует шести уравнениям равновесия:
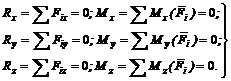 (19)
(19)
Итак, для равновесия произвольной пространственной системы сил необходимо и достаточно, чтобы алгебраическая сумма проекций всех сил на каждую из трех осей координат равнялась нулю и чтобы алгебраическая сумма моментов всех сил относительно каждой из трех осей координат равнялась нулю. В частном случае, если линии действия всех сил параллельны, выбрав ось z параллельно силам, а оси х и у перпендикулярно силам, получим следующие условия равновесия:

|
Из за большого объема этот материал размещен на нескольких страницах:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 |




