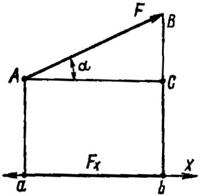
Рис. 17
Проекция силы на ось есть величина скалярная. Она может быть положительной, отрицательной или равной нулю в зависимости от величины угла a между направлением силы и положительным направлением оси. Из прямоугольного треугольника ABC следует, что Fx = F сos a, т. е. проекция силы на ось равна произведению модуля силы на косинус угла между направлением силы и положительным направлением оси.
Если угол a острый, то проекция положительна (рис. 17), если угол a – тупой, то проекция отрицательна (рис. 18, а):
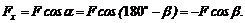
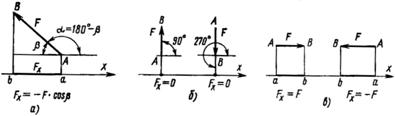
Рис. 18
Нетрудно убедиться, что проекция силы на ось будет равна нулю, если a = 90° или 270° (рис. 18, б), и равна модулю силы, если a = 0 или a = 180° (рис. 18, в).
Модуль и направление силы можно определить по ее проекциям на две взаимно перпендикулярные оси (рис. 18, в):
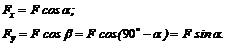
Из треугольника ABC, поскольку АС = Fx и ВС = Fy, следует, что модуль силы F равен
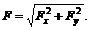 (3)
(3)
Направление силы определяют косинусы углов (рис. 19):
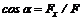 ;
; 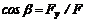 . (4)
. (4)
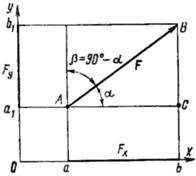
Рис. 19
Задача 10. В точке В кронштейна ABC (рис. 20, а) подвешен груз М весом 8 кН. Определить реакции стержней кронштейна, если углы кронштейна a = 110°, b = 30° и крепления в точках А, В и С шарнирные.
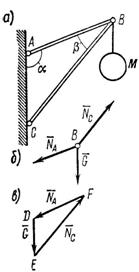
Рис. 20
Решение – методом проекций при помощи уравнений равновесия.
1. Так как три силы ![]() , и , действующие на точку В (рис. 21), образуют уравновешенную систему, то алгебраические суммы проекций этих сил на каждую из двух осей координат равны нулю.
, и , действующие на точку В (рис. 21), образуют уравновешенную систему, то алгебраические суммы проекций этих сил на каждую из двух осей координат равны нулю.
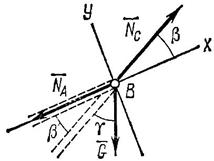
Рис. 21
2. Выберем оси координат так, чтобы одна из осей совпадала с линией действия одной из неизвестных сил (рис. 21), и составим два уравнения равновесия:
 (1)
(1)
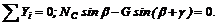 (2)
(2)
Из уравнения (2)
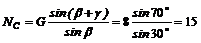 кН.
кН.
Из уравнения (1)
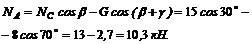
Задача 11. К шарниру В кронштейна ABC прикреплена веревка, перекинутая через блок, к другому концу которой прикреплен груз весом G = l,5 кН (рис. 22). Определить усилия в стержнях АВ и СВ кронштейна, если крепления в точках А и С шарнирные, a = 35° и b = 100°.
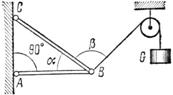
Рис. 22
Решим задачу методом проекций.
1. Изобразив шарнир В вместе с действующими на него силами ![]() и и расположив оси проекций, как показано на рис. 19, составим уравнения равновесия:
и и расположив оси проекций, как показано на рис. 19, составим уравнения равновесия:
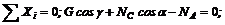 (1)
(1)
![]() (2)
(2)
2. Из уравнения (2)
 кН,
кН,
а из уравнения (1)
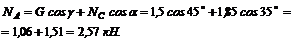
Итак, реакции стержней (их действия на шарнирный болт В) равны NA = 2,57 кН и NС = l,85 кН. Точно с такими же усилиями действует шарнирный болт на стержни. Стержень АВ растянут силой 2,57 кН, а стержень СВ сжат силой 1,85 кН.
В связи с решением подобных задач методом проекций необходимо отметить следующее. Применяя метод проекций к определению равнодействующей любого числа сходящихся сил, наиболее удобно использовать обычную прямоугольную систему координатных осей. При этом найденные проекции равнодействующей и искомая равнодействующая образуют прямоугольный треугольник, решая который легко определить модуль и направление равнодействующей. Применяя метод проекций к решению задач на равновесие сил, совсем не обязательно использовать взаимно перпендикулярные оси.
В тех случаях, когда определяются модули сил, направления которых заданы, каждую из осей целесообразно расположить перпендикулярно к направлению искомых сил. Тогда в каждое уравнение равновесия войдет только одно неизвестное.
§ 5. Условия равновесия плоской системы сходящихся сил
Если система сходящихся сил находится в равновесии, то ее равнодействующая R = 0, следовательно,
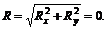
Очевидно, что данное выражение будет обращаться в нуль, если
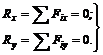 (5)
(5)
Можно применить упрощенную запись 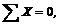
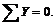 Уравнения (5) выражают условия равновесия плоской системы сходящихся сил в аналитической форме.
Уравнения (5) выражают условия равновесия плоской системы сходящихся сил в аналитической форме.
Для равновесия плоской системы сходящихся сил необходимо и достаточно, чтобы алгебраические суммы проекций этих сил на каждую из двух координатных осей равнялись нулю.
Метод проекций при решении задач на равновесие системы особенно удобен в том случае, если в систему входит более трех сил.
Задача 12. На оси шарнира В (рис. 23) шарнирно-стержневой системы ABC свободно вращается блок. Через блок перекинута нить, с помощью которой удерживается груз весом G = 50 Н. Определить усилия в стержнях АВ и ВС. При этом диаметром блока и трением нити можно пренебречь.
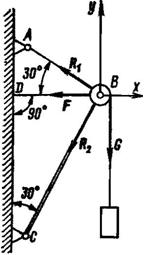
Рис. 23
Решение.
1. Выделить точку, равновесие которой следует рассмотреть. В данной задаче это будет точка В неподвижного блока.
2. Изобразить векторы всех активных сил, действующих на нее. В нашем примере это натяжение вертикальной ветви нити, равное весу груза, и натяжение горизонтальной ветви нити.
3. Мысленно отбросить связи и заменить их реакциями R1 и R2.
4. Все силы изобразить в виде векторов (рис. 23).
Предположив, что стержни АВ и ВС растянуты, направить соответственно реакции R1 и R2 от узла В.
5. Выбрать направление координатных осей х и у.
6. Составить два уравнения равновесия:
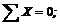
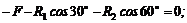
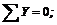
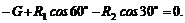
Учитывая, что F = G = 50 H, и решая совместно оба уравнения, получим R1 = – 18,6 H; R2 = – 68,5 Н. Здесь знаки «минус» указывают, что стержни АВ и ВС сжаты, а не растянуты, как мы предполагали заранее.
Глава 2. ПЛОСКАЯ СИСТЕМА ПРОИЗВОЛЬНО РАСПОЛОЖЕННЫХ СИЛ
§ 6. Момент силы относительно точки
Если к телу, закрепленному при помощи шарнира (рис. 24), приложить силу F, то эта сила будет стремиться вращать тело относительно центра шарнира О (вокруг оси, перпендикулярной к плоскости чертежа).
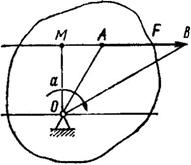
Рис. 24
Вращающее действие силы измеряют величиной, называемой моментом силы. Момент силы относительно точки равен произведению модуля силы на кратчайшее расстояние от данной точки до линии действия силы.
Величину момента обозначают буквой М, а расстояние ОМ от точки до линии действия силы, которое называют плечом силы, – буквой а. Точку О называют центром момента. Чтобы найти плечо силы, нужно опустить перпендикуляр из центра момента на линию действия силы F. Момент силы принято считать положительным, если сила стремится вращать тело вокруг центра моментов (в плоскости чертежа) по часовой стрелке, и отрицательным – в противном случае. Таким образом, в общем виде
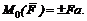 (6)
(6)
Так как сила измеряется в ньютонах, а расстояние в метрах, то момент имеет размерность: Н×м.
Момент силы относительно точки можно рассматривать как удвоенную площадь треугольника АОВ (см. рис. 24):
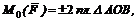
где АВ – основание треугольника, а ОМ – его высота.
Из определения момента силы относительно точки очевидно следующее:
модуль и знак момента не изменяются при переносе силы по линии ее действия либо центра моментов по прямой, параллельной линии действия силы;
момент силы относительно точки равен нулю, если центр моментов лежит на линии действия силы.
Задача 13. Определить моменты сил F1, F2, F3, F4 относительно точки А (рис. 25), если АВ = 0,7 м; AD = 0,4 м; АС = 0,2 м; F1 = 10 Н; F2 = 25 Н; F3 = 5 Н; F4 = 8 Н.

|
Из за большого объема этот материал размещен на нескольких страницах:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 |




