Решение.
1. В данном случае движение точки А вместе с кривошипом можно считать сложным, т. е. получающимся в результате сложения:
а) движения точки А вместе с кулисой в ее возвратно-поступательном (переносном) движении вдоль оси х;
б) относительного движения точки А вместе с камнем, движущимся возвратно-поступательно в прорези кулисы в направлении, перпендикулярном к оси х.
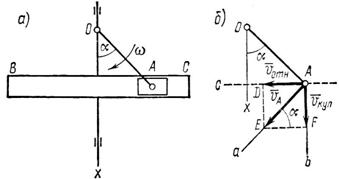
Рис. 80
2. Абсолютная скорость точки А, модуль которой легко определяется по формуле 
направлена перпендикулярно к кривошипу ОА. Переносная скорость точки А, равная поступательной скорости кулисы 
направлена по прямой АВ (рис. 80 , б). Относительная скорость 
точки А, равная скорости камня в прорези кулисы, направлена по прямой АС.
3. Изобразим скорость vА= 4 м/сек вектором, перпендикулярным к ОА. Разложим ее на составляющие и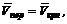 
как показано на рис. 76, б. Вектор изображает искомую скорость кулисы.
4. 
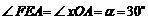(как углы с взаимно перпендикулярными сторонами) и, следовательно,
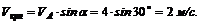
Таким образом, в данный момент кулиса перемещается вниз со скоростью 2 м/с.
Чтобы лучше проанализировать движение кулисы, необходимо знать, когда кулиса двигается ускоренно, когда замедленно, при каких положениях кривошипа кулиса имеет максимальную скорость и чему равна эта скорость, при каких положениях кривошипа скорость кулисы равна нулю?
Глава 6. СЛОЖНОЕ ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА
§ 22. Плоскопараллельное движение тела
Подобно сложному движению точки движение тела относительно неподвижной системы отсчета удобно в некоторых случаях считать сложным, т. е. состоящим из относительного и переносного движений. Обычно составляющие части сложного движения – это простейшие движения тела: поступательное и вращательное.
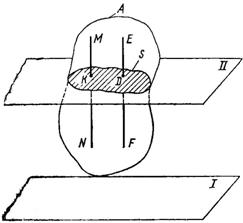
Рис. 81
Рассмотрим один из случаев сложного движения тела, широко встречающийся в технике – это так называемое плоскопараллельное движение. Оно получается в том случае, когда все точки движущегося твердого тела перемещаются в плоскостях, параллельных данной неподвижной плоскости. Таково, например, движение шатуна в кривошипно-шатунном механизме, движение сателлитов в планетарном механизме, качение колеса по прямолинейному рельсу и т. д.
Пусть твердое тело А (рис. 81) движется параллельно неподвижной плоскости I. Пересечем тело плоскостью II, параллельной плоскости I. Получим в сечении фигуру S, которая, перемещаясь вместе с телом, остается все время в плоскости II.
Отрезок MN, проведенный перпендикулярно к плоскости сечения S, во время движения остается все время перпендикулярным к плоскостям II и I, т. е. перемещается параллельно своему первоначальному положению – значит, движется поступательно. Все точки прямой MN, а следовательно, и точка К, лежащая в плоскости фигуры S, имеют одинаковые траектории скорости и ускорения.
Аналогичные рассуждения можно привести в отношении прямой EF и любой другой прямой тела А.
Так как движение точки К такое же, как и всех точек, лежащих на прямой MN, а движение точки D – всех точек прямой EF, то, очевидно, можно утверждать, что движение фигуры S в плоскости II определяет движение всего тела А. Поэтому для изучения плоскопараллельного движения тела достаточно изучить движение плоской фигуры в ее плоскости.
Рассмотрим движение фигуры S (рис. 82) в плоскости II относительно неподвижно связанных с этой плоскостью осей хОу. Пусть оси x1O1y1 будут связаны с движущейся фигурой S – это подвижные оси.
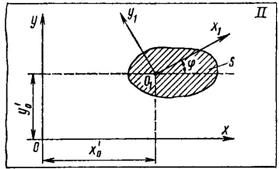
Рис. 82
Положение фигуры S в ее плоскости будет определяться положением подвижной системы осей относительно неподвижной, т. е. координатами центра 01 и углом поворота j. Иначе, положение фигуры S в данный момент времени можно определить, если будут известны функции
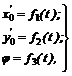(39)
которые называют уравнениями плоскопараллельного движения. Если при движении будет оставаться постоянным угол j (j = const), то тело движется поступательно и уравнениями его движения будут функции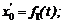 
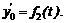Если при движении не будут изменяться координаты центра О, т. е. 
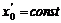и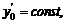 
то тело совершает вращательное движение, которое описывается уравнением j = f(t).
Приведенные рассуждения позволяют сделать вывод, что поступательное и вращательное движения можно рассматривать как частные случаи плоскопараллельного движения тела.
§ 23. Определение скорости точки тела
при плоскопараллельном движении
Рассмотрим движение плоской фигуры в своей плоскости (рис. 83). Пусть полюсом служит точка А. Сложное движение фигуры состоит из поступательного вместе с полюсом со скоростью VA и вращательного вокруг этого полюса с угловой скоростью w. Поступательное движение является переносным, вращательное – относительным. Теперь мы можем найти абсолютную скорость любой другой точки тела В как геометрическую сумму двух скоростей: переносной скорости поступательного движения, равной скорости полюса: VBпер = VA, и относительной скорости вращательного движения вокруг полюса: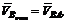 
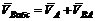. (40)
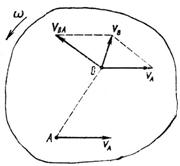
Рис. 83
Причем вектор перпендикулярен радиусу вращения АВ и направлен в сторону вращения. Модуль его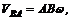 
где w – угловая скорость тела. При решении таких задач обычно в качестве полюса принимают точку, скорость которой в данный момент времени известна.
Задача 54. В четырехзвенном механизме (рис. 84) кривошип ОА вращается равномерно с частотой п = 300 об/мин. Для заданного положения механизма, при котором кривошип ОА перпендикулярен шатуну АВ и < ABC = 45°, определить угловую скорость звена (коромысла) ВС, если ОА = 0,12 м, АВ = 0,3 м и ВС = 0,14 м.
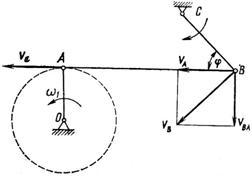
Рис. 84
Решение.
1. Шатун механизма АВ совершает плоскопараллельное движение. Выберем в качестве полюса точку А, скорость которой VA направлена перпендикулярно радиусу кривошипа ОА в сторону вращения, модуль последней легко определить из выражения:
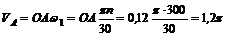м/с.
2. Абсолютную скорость точки В шатуна найдем как геометрическую сумму двух составляющих скоростей: поступательного движения, равной VА, и окружной относительно полюса – VВА, направленной перпендикулярно АВ. Точка В принадлежит коромыслу ВС, которое совершает вращение относительно центра С, следовательно, ее абсолютная скорость VВ направлена перпендикулярно ВС и также направлена в сторону его вращения. Учитывая это, построим параллелограмм, диагональю которого будет вектор VВ, а сторонами векторы VВА и VA.
Угол между VВ и VA равен 45°, поэтому
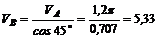м/с.
3. Искомую угловую скорость коромысла найдем из выражения
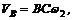
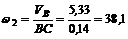рад/с.
§ 24. Мгновенный центр скоростей
Определим в данный момент времени абсолютную скорость некоторой точки С плоской фигуры, которая лежит на прямой, перпендикулярной вектору скорости полюса V0. Причем, пусть расстояние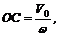 
где w – угловая скорость фигуры (рис. 85). Нетрудно убедиться, что абсолютная скорость этой точки будет равна нулю, так как направления векторов относительной скорости Vco и переносной V0 противоположны, а их модули равны.
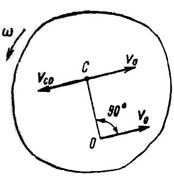
Рис. 85
Действительно,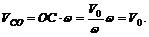 
Очевидно, если скорость некоторой точки С движущейся фигуры равна нулю, то фигура в данный момент времени совершает вращательное движение вокруг рассматриваемой точки (либо твердое тело вращается вокруг оси, проходящей через точку С перпендикулярно плоскости чертежа). Эту точку называют мгновенным центром скоростей (МЦС), или мгновенным центром вращения.
|
Из за большого объема этот материал размещен на нескольких страницах:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 |
