Решение.
1. Рассматривая доску как рычаг, видим, что на нее действуют три нагрузки: вес левого груза G1 = mlg, вес правого груза G2 = m2g и собственный вес доски Gд = mдg (рис. 34, б).
2. Для равновесия доски необходимо, чтобы алгебраическая сумма моментов этих сил относительно опоры В равнялась нулю. Следовательно,
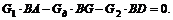
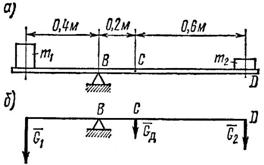
Рис. 34
3. Подставив вместо весов их выражения через массы и разделив обе части равенства на постоянную величину g (ускорение свободного падения 9,81 м/сек2), получим
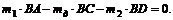
4. Отсюда находим массу доски:
![]()
§ 9. Уравнения равновесия произвольной плоской системы сил
Произвольная плоская система сил будет в равновесии, если главный вектор и главный момент системы будут равны нулю, т. е. R = 0 и М = 0. Эти условия являются необходимыми и достаточными. Действительно, равенство R = 0 означает, что геометрическая сумма сил системы, перенесенных в произвольно выбранный центр приведения, равна нулю, т. е. эти силы уравновешены. Из равенства М = 0 следует, что сумма моментов присоединенных пар равна нулю, а это есть необходимое и достаточное условие равновесия системы пар.
Выше было показано, что модуль главного вектора системы можно определить по его проекциям на оси координат:
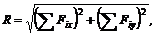
а модуль главного момента системы:
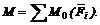
Поэтому выражение условия равновесия системы можно записать в следующей форме:
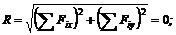
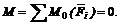
Откуда следует, что для равновесия плоской системы произвольно расположенных сил необходимы и достаточны три условия:
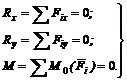 (11)
(11)
Сокращенная запись условий:
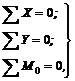 (12)
(12)
т. е. алгебраическая сумма проекций всех сил системы на ось х равна нулю; алгебраическая сумма проекций всех сил системы на ось у равна нулю; алгебраическая сумма моментов всех сил системы относительно любой точки равна нулю.
Первые два уравнения равновесия называют уравнениями проекций, третье – уравнением моментов.
Наряду с этой основной формой уравнений плоской системы сил можно доказать справедливость еще двух форм.
Первая форма уравнений:
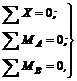 (13)
(13)
т. е. для равновесия произвольной плоской системы необходимо и достаточно, чтобы равнялись нулю алгебраические суммы моментов всех сил относительно двух точек плоскости и алгебраическая сумма проекций всех сил на одну ось, но не перпендикулярную к прямой, соединяющей центры моментов А и В.
Вторая форма уравнений:
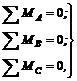 (14)
(14)
т. е. для равновесия произвольной плоской системы сил необходимо и достаточно, чтобы алгебраические суммы моментов относительно трех точек плоскости, но не лежащих на одной прямой, равнялись нулю.
Нетрудно убедиться, что плоская система сходящихся сил и плоская система пар являются частными случаями произвольной плоской системы сил. Действительно, если за центр приведения выбрать точку пересечения линий действия всех сил, главный момент системы относительно этой точки равен нулю и система сводится к одному главному вектору. Для равновесия необходимо удовлетворение только двух условий: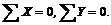 Плоская система пар, как известно, сводится только к результирующей паре, а главного вектора не существует. Следовательно, для равновесия системы пар необходимо и достаточно только одно условие:
Плоская система пар, как известно, сводится только к результирующей паре, а главного вектора не существует. Следовательно, для равновесия системы пар необходимо и достаточно только одно условие: 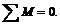
Существует еще третий частный случай – это система параллельных сил.
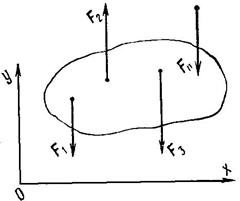
Рис. 35
Пусть к телу будет приложена система сил F1, F2, F3, …, Fn, линии действия которых параллельны друг другу (рис. 35). Так как ось х перпендикулярна всем силам, то условие 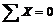 будет всегда выполняться, даже если система не уравновешена. Следовательно, условия равновесия плоской системы параллельных сил выражаются уравнениями
будет всегда выполняться, даже если система не уравновешена. Следовательно, условия равновесия плоской системы параллельных сил выражаются уравнениями
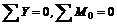
или
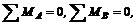
где А и В – произвольно выбранные точки на плоскости.
Задачи на равновесие произвольной плоской системы сил должны содержать не более трех неизвестных, а на равновесие плоской системы параллельных сил – не более двух неизвестных. Если неизвестных больше, чем уравнений статики, то задача становится статически неопределимой, для ее решения потребуются дополнительные уравнения, которые будут рассмотрены в разделе 2.
Для решения задачи составляют уравнения равновесия одним из трех указанных способов. Для проверки правильности решения задачи можно составить четвертое уравнение равновесия из числа неиспользованных в ходе решения задачи.
Задача 19. Однородный брус АВ (рис. 36) весом G = 250 Н прикреплен к стене при помощи шарнира А и в точке D опирается на гладкий цилиндр. В точке Е к брусу подвешен груз Р = 800 Н. Определить реакцию цилиндра и шарнира, если АЕ = 1,2 м; АС = ВС = 1,5 м; AD = 1,7 м и Ð ВАх = a = 40°.
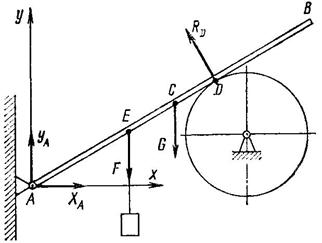
Рис. 36
Решение.
1. Рассмотрим равновесие бруса АВ.
2. Приложим к брусу активные силы: собственный вес G в центре тяжести С (для однородного бруса центр тяжести расположен посередине) вертикально вниз и силу F – от веса груза.
3. Связями для бруса являются цилиндр и шарнир. Мысленно освобождаемся от связей и заменяем их реакциями. Реакция гладкого цилиндра RD направлена по нормали к поверхности цилиндра в точке касания D. Реакция шарнира RA приложена в центре шарнира А. Так как направление реакции неизвестно, заменим ее двумя составляющими Rx и Ry, направив их по осям Ох и Оу. Направление осей показано на рис. 36. Центр моментов выбираем в точке А.
4. Составим три уравнения равновесия, так как активные силы и реакции связей составляют произвольную плоскую систему сил:
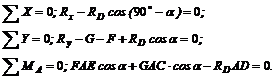
Из третьего уравнения находим RD:
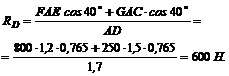
Из первого уравнения
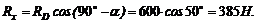
Из второго уравнения
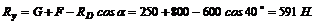
Для проверки правильности решения составим уравнение моментов относительно точки С:
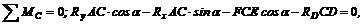
где
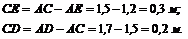
Подставим в уравнение 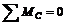 найденные значения сил Rx, Ry и RD:
найденные значения сил Rx, Ry и RD:
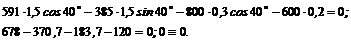
Уравнение превратилось в тождество, следовательно, задача решена верно.
Задача 20. На горизонтальную балку АВ, левый конец которой имеет шарнирно-неподвижную опору, а правый – шарнирно-подвижную, в точках С и D поставлены два груза: P1=10 кН и P2 = 20 кH (рис. 37, а). Определить реакции опор балки.
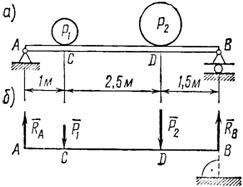
Рис. 37
Решение.
1. Рассмотрим равновесие балки AB, на которую в точках С и D действуют две вертикальные нагрузки ![]() и
и ![]() (рис. 37, б).
(рис. 37, б).
2. Освободив правый конец балки от связи и заменив ее действие реакцией , направленной перпендикулярно к опорной поверхности, увидим, что на балку действует система параллельных сил. Поэтому, если освободить и левый конец балки от шарнирно-неподвижной опоры, то ее реакция будет также направлена вертикально (рис. 37, б).
3. Составим систему уравнений равновесия, приняв для одного уравнения за центр моментов точку А, а для другого – точку В:
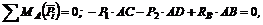 (1)
(1)
 (2)
(2)
4. Решая уравнения, из (1) находим
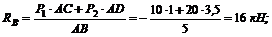
из (2)
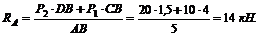
5. Проверим правильность решения, составив уравнение проекций сил на вертикальную ось у:

|
Из за большого объема этот материал размещен на нескольких страницах:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 |




