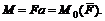
В частном случае, если центр приведения выбрать на линии действия силы F, то момент присоединенной пары будет равен нулю. Значит, присоединять пару необходимо только при параллельном переносе силы.
Рассмотрим теперь произвольную плоскую систему из n числа сил (F1, F2, F3, ..., Fn) (рис. 28). Выберем на плоскости произвольную точку О и перенесем в нее все силы системы. В результате приведения получим пучок приложенных в точке О сил (F'1, F'2, F'3, ..., F'n) и систему присоединенных пар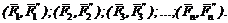 
Моменты этих пар соответственно равны:
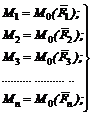(7)
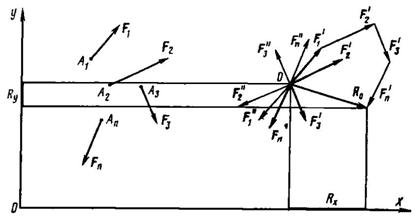
Рис. 29
Сложим все силы пучка при помощи построения силового многоугольника (рис. 29) и получим их равнодействующую R0:
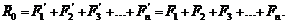
Затем сложим все присоединенные пары и получим одну равнодействующую пару с моментом М = М1 + М2 + М3 + ... + Мп. Итак, произвольная система сил эквивалентна одной силе и одной паре, которые носят название главный вектор и главный момент системы.
Можно сказать, что главный вектор – это вектор, представляющий собой геометрическую сумму всех заданных сил, перенесенных параллельно самим себе в точку О, называемую центром приведения.
Модуль главного вектора можно определить по его проекциям Rx и Ry на оси координат Ох и Оу (см. рис. 29) по формуле 
где на основании теоремы о проекции равнодействующей на ось:
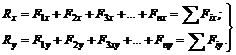(8)
Направление главного вектора определяется из выражени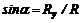й 
и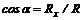 
, где a – угол между главным вектором и положительным направлением оси х.
Модуль главного момента системы получим, используя уравнения (7):
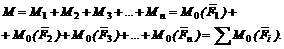(9)
Откуда модуль главного момента системы равен алгебраической сумме моментов всех сил системы относительно центра приведения.
Если за центр приведения принять другую точку, то нетрудно убедиться, что модуль и направление главного вектора будет таким же, т. е. они не зависят от выбора центра приведения.
Что же касается главного момента системы, то его модуль и направление зависят от выбора центра приведения, так как при изменении положения центра приведения изменяются плечи сил заданной системы, а следовательно, и их моменты. Следует также отметить, что главный вектор не является равнодействующей системы, хотя по модулю и направлению совпадает с ней. Рассмотренный случай приведения системы, когда R0 ¹0 и М¹0, является общим.
Возможны следующие частные случаи приведения:
а) главный вектор оказался равным нулю, а главный момент не равен нулю (R0 = 0, М ¹ 0), т. е. система эквивалентна одной только паре;
б) главный вектор не равен нулю, а главный момент равен нулю (R0 ¹ 0, М = 0), т. е. система сводится к одной силе, и очевидно, что главный вектор есть равнодействующий этой системы;
в) главный вектор и главный момент системы равны нулю (R0 = 0, М = 0) – система находится в равновесии.
§ 8. Равнодействующая плоской системы сил.
Теорема Вариньона о моменте равнодействующей
Рассмотрим более подробно общий случай приведения системы, когда R0 ¹ 0 и М ¹ 0. Можно убедиться, что в этом случае система имеет равнодействующую, приложенную в некоторой точке, не совпадающей с центром приведения.
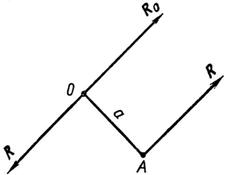
Рис. 30
Пусть данная система сил приведена к главному вектору R0, приложенному в точке О (рис. 30), и главному моменту системы М (пара RR'). Представим последний в виде пары сил, у которых модуль равен модулю главного вектора системы. Одну из сил пары R' приложим в центре приведения О и направим противоположно главному вектору системы. Тогда точку приложения второй силы пары R найдем, если вычислим плечо пары:
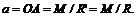
Силы R0 и R', равные и противоположно направленные, взаимно уравновешиваются, их можно отбросить согласно 2-й аксиоме статики. Остается одна сила R = R0, заменившая собой заданную систему сил. Она и является равнодействующей этой системы. Таким образом, мы доказали, что в общем случае, когда главный вектор и главный момент системы не равны нулю, система имеет равнодействующую, равную по модулю и направленную параллельно главному вектору в ту же сторону.
Модуль момента равнодействующей R относительно центра приведения О:
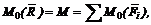
но произведение Ra выражает модуль главного момента системы, следовательно, учитывая выражение (9), имеем
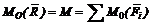. (10)
Следовательно, момент равнодействующей произвольной плоской системы сил относительно любого центра равен алгебраической сумме моментов всех сил системы относительно этого же центра (теорема Вариньона).
Плоскую систему сходящихся сил и плоскую систему параллельных сил следует рассматривать как частные случаи произвольной системы. Для них также справедлива теорема Вариньона.
Теоремой Вариньона широко пользуются при решении различных задач статики. В частности, ее применяют при определении равнодействующей системы параллельных сил.
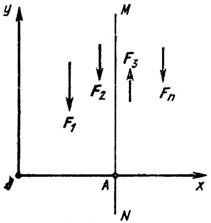
Рис. 31
Пусть задана плоская система параллельных сил (рис. 31). Найдем главный вектор этой системы по его проекциям на оси координат, направив ось Оу параллельно, а ось Ох – перпендикулярно данным силам. При этом будем учитывать, что главный вектор равен по модулю равнодействующей системы, параллелен ей и направлен в ту же сторону:
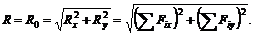
Так как то вектор равнодействующей направлен параллельно составляющим силам, а модуль ее
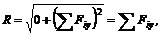
т. е. модуль равнодействующей системы параллельных сил равен алгебраической сумме проекций сил системы на ось, параллельную этим силам. Знак алгебраической суммы показывает, в какую сторону направлена равнодействующая: «плюс» – равнодействующая направлена в сторону положительного направления оси проекции, «минус» – в противоположном направлении. Выбрав центр моментов в произвольной точке О, по теореме Вариньона найдем расстояние ОА, определяющее положение линии действия равнодействующей R.
Задача 16. К телу в точках А и В приложены параллельные силы F1 = 20 Н, F2 =60 H и F3 = 18 Н (рис. 32). Определить модуль, направление и линию действия равнодействующей.
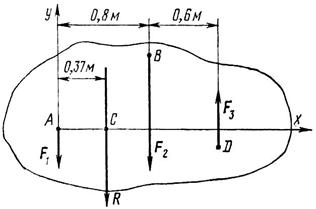
Рис. 32
Решение.
1. Приняв точку А за начало координат, направим ось х перпендикулярно данным силам, а ось у параллельно им.
2. Найдем модуль равнодействующей:
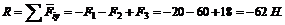
Так как знак алгебраической суммы проекций получился отрицательным, то вектор равнодействующей направлен вниз, в сторону отрицательного направления оси Y.
3. Приняв точку A за центр моментов, на основании теоремы Вариньона запишем:
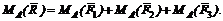
Учитывая, что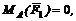 
найдем расстояние АС между линиями действия и равнодействующей из выражения
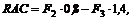
откуда
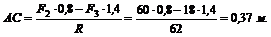
Задача 17. Определить равнодействующую двух параллельных сил и , направленных в одну сторону (рис. 33, а) если P1 = 12 H и P2 = 15 H.
Решение.
1. Примем за начало осей проекций точку А. Ось x расположим перпендикулярно к данным силам и направим ее вправо, а ось у направим вдоль силы вниз (рис. 33, б).
2. Найдем модуль равнодействующей:
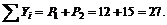
Следовательно, R = 27 H.
Так как сумма проекций положительна, то вектор равнодействующей направлен тоже вниз.
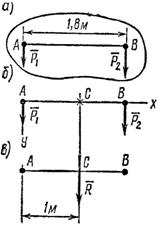
Рис. 33
3. Приняв за центр моментов точку А, найдем расстояние АС от точки А до линии действия равнодействующей.
В данном случае ,
но
поэтому Откуда
Таким образом, равнодействующая двух данных сил численно равна 27 Н, и линия ее действия расположена от точки А на расстоянии АС = 1 м (рис. 33, в).
Задача 18. Какова должна быть масса однородной доски (рис. 34, а), чтобы, опираясь в точке В на гладкую опору, она с положенными на нее грузами т1 = 100 кг и m2 = 48 кг находилась в равновесии? Центр тяжести доски расположен в точке С.
|
Из за большого объема этот материал размещен на нескольких страницах:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 |
