Пусть твердое тело вращается вокруг неподвижной оси Оz (рис. 69). Проведем через ось вращения неподвижную плоскость Q и плоскость Р, жестко связанную с телом. При вращении тела угол j между плоскостями будет непрерывно меняться с течением времени. Его называют углом поворота тела и измеряют в радианах.
Зависимость угла поворота от времени описывается уравнением
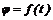, (30)
которое называют законом вращательного движения.
Быстроту и направление вращения можно охарактеризовать с помощью угловой скорости w. Модуль угловой скорости определяют как быстроту изменения функции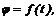 
т. е. как первую производную от угла поворота по времени:
. (31)
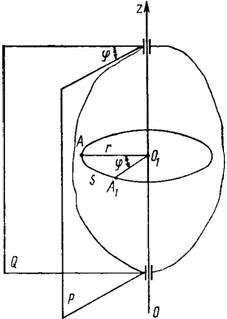
Рис. 65
Угловую скорость измеряют в рад/с. В общем случае при неравномерном вращении угловая скорость изменяется с течением времени, т. е.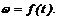 
Характеристикой быстроты изменения угловой скорости является угловое ускорение, равное первой производной от угловой скорости по времени:
, (32)
которое измеряют в рад/c2.
Если знаки w и e одинаковы, то имеет место ускоренное вращение, если знаки w и e различны – замедленное вращение.
§ 19. Частные случаи вращательного движения
Если модуль угловой скорости при вращении тела постоянен (w = const), то имеет место равномерное вращение. Угловую скорость равномерного вращения находят как отношение угла поворота за некоторый промежуток времени к этому промежутку, т. е.
, (33)
откуда
(34)
Последнее уравнение называют законом равномерного вращения.
Иногда удобно угловую скорость равномерного вращения выражать через число п оборотов, совершаемых в одну минуту. Число оборотов в минуту называют частотой вращения. За один оборот тело поворачивается на 2p радиан, а за п оборотов на 
радиан. В одной минуте 60 с, поэтому
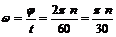, (35)
откуда частота вращения
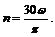
Если при вращении угловое ускорение остается без изменения (e = const), то имеет место равномерно-переменное вращение.
Формулы для определения угла поворота и угловой скорости при равномерно-переменном вращательном движении аналогичны формулам для равномерно-переменного движения точки, только вместо величины s, V, V0, at нужно подставить величины j, w, w0 и e. В результате получим:
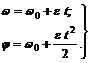(36)
Причем, если w0 > 0 и e > 0 – движение равномерно ускоренное, а если w0 > 0 и e < 0 – движение равномерно замедленное.
Задача 41. В период разгона маховик вращается вокруг своей оси по закону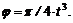 
Определить угловую скорость и угловое ускорение маховика в момент, когда он сделает 27 оборотов.
Решение:
1. Найдем угол поворота маховика за время разгона: j = 27 оборотов = 27 - 2p = 54p рад.
2. Определим время разгона: 54p = p / 4 × t3, откуда
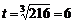с.
3. Определим угловую скорость в момент t = 6 с:
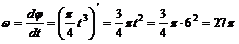рад/с.
4. Определим угловое ускорение в момент t = 6 с:
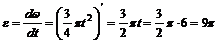рад/с2.
Задача 42. Вал, диаметр которого 0,06 м, вращается равномерно с частотой 1200 об/мин. Определить скорость и ускорение точек вала на его поверхности (рис. 70).
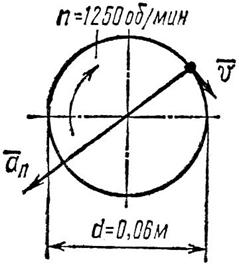
Рис. 70
Решение.
1. Скорость точки вращающегося тела можно найти по формуле
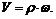
2. Но известно, что
.
3. Подставим сюда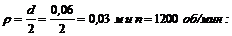 
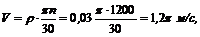
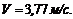
Вал вращается равномерно, следовательно скорость точек остается численно неизменной. По этой же причине у точек отсутствует касательное ускорение.
5. Нормальное ускорение найдем из формулы
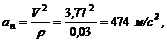
которое также в данном случае остается по модулю неизменным.
Задача 43. Дисковая пила 1 имеет диаметр 600 мм. На валу пилы насажен шкив 2 диаметром 300 мм, а шкив соединен бесконечным ремнем со шкивом двигарис. 71) диаметром 120 мм. С какой угловой скоростью должен вращаться шкив двигателя, чтобы скорость зубьев пилы не превышала 15 м/с?
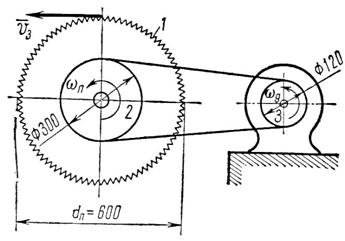
Рис. 71
Решение.
1. Так как пила 1 и шкив 2 насажены на одном валу, то они имеют одну и ту же угловую скорость wп и скорость зубьев пилы V3 = 15 м/с зависит от wп:
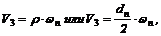
потому что
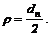
2. Находим угловую скорость шкива 2, который обеспечивает необходимую рабочую скорость зубьев пилы:
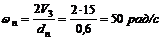
(dп = 600 мм = 0,6 м).
3. Теперь найдем угловую скорость wд шкива двигателя. Шкивы 2 и 3 соединены бесконечным ремнем. Полагая, что ремень не растягивается и не проскальзывает на шкивах, можно считать, что все его точки движутся с одной и той же скоростью Vр. Это означает, что скорости точек, расположенных на поверхностях обоих шкивов, одинаковы и равны Vр.
Поэтому применим зависимость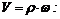 
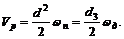
Отсюда
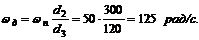
4. Если перевести эту угловую скорость в об/мин, то
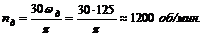
Таким образом, для того чтобы зубья пилы имели скорость 15 м/с, шкив двигателя должен вращаться с угловой скоростью 125 рад/с (или 1200 об/мин).
Задача 44. Маховик, вращающийся с частотой n0 = 90 об/мин, с некоторого момента начинает вращаться равноускоренно и через 1,5 мин достигает скорости вращения пк = 150 об/мин. Определить угловое ускорение маховика. Сколько всего оборотов делает маховик за 1,5 мин? Какую скорость имеют точки на цилиндрической поверхности маховика через 45 с после начала равноускоренного движения, если диаметр маховика 1,2 м?
Решение.
Все угловые величины выражаем в радианном измерении.
1. Если n0 = 90 об/мин, то
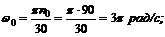
если пк = 150 об/мин, то
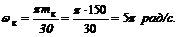
2. Находим угловое ускорение, учитывая, что изменение угловой скорости от w0 до wк происходит за t = 1,5 мин = 90 с:
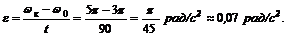
3. Определяем угол поворота тела за t= 1,5 мин =90 с, принимая j0 = 0:
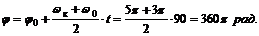
4. Находим, какому числу оборотов соответствует этот угол поворота:
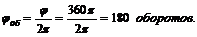
Следовательно, за время равноускоренного вращения маховик успеет совершить 180 оборотов.
5. Прежде чем найти по формуле V] = w1r скорость точек на ободе маховика в момент времени t = 45 с после начала равноускоренного вращения, необходимо найти угловую скорость маховика w1 в этот момент:
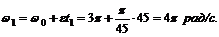
Зная, что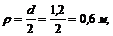 
получаем
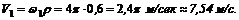
Решение 2 – угловые величины выражаются в оборотах, а время – в сек (t = 1,5 мин = 90 сек).
1. Выражаем данные скорости вращения в об/с.
n0 = 90 об/мин = 1,5 об/сек и nк = 150 об/мин = 2,5 об/с.
2.Определим угол поворота в ином виде, приняв j0 = 0:
.
Тогда
|
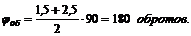
Из за большого объема этот материал размещен на нескольких страницах:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 |
