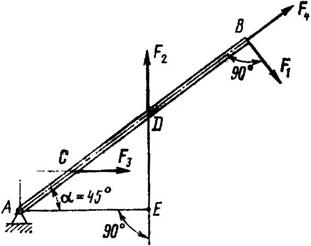
Рис. 25
Решение.
1. Момент силы F1 относительно точки А положительный, а плечо силы равно АВ, поэтому
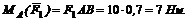
2. Момент силы F2 относительно точки А отрицательный, так как сила F2 стремится вращать тело АВ против часовой стрелки. Из треугольника ADE плечо силы F2 АЕ = AD cos 45°, следовательно,
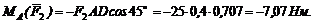
3. Момент силы F3 относительно точки А положительный. Из треугольника АКС плечо силы F3 AK = ACcos 45°, следовательно,
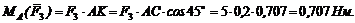
Линия действия силы F4 пересекает центр моментов, значит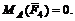 
Задача 14. Определить моменты шести заданных сил (рис. 26) относительно точек А, В и С, если P1 = 30 Н, Р2 = 50 Н, Р3 = 25 Н, Р4 = = 40 Н, Р5 = 35 Н, Р6 = 54 Н, АВ = 1,2 м, ВС = 0,8 м, a = 55° и b = 35°.
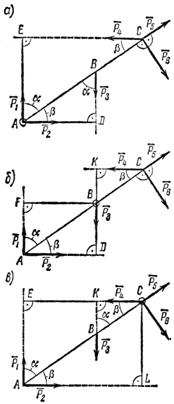
Рис. 26
Решение 1 – определение моментов шести заданных сил относительно точки А (рис. 26, а).
1. Центр моментов в точке А. Через точку А проходят линии действия трех сил 
, и 
Значит для этих сил плечи равны нулю. Следовательно,
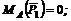
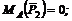
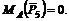
2. Находим момент силы 
. Опустив из точки А на линию действия силы перпендикуляр AD, получим плечо силы Длину AD легко найти, так как это катет треугольника ABD:
3. Величина момента отрицательная (сила поворачивает плечо AD вокруг точки А по ходу часовой стрелки), следовательно,
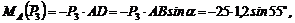
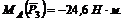
4. Находим момент силы Плечом силы является перпендикуляр АЕ к СЕ – линии действия силы Из треугольника АСЕ
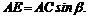
Величина момента положительная (плечо АЕ поворачивается около точки А силой против хода часовой стрелки). Следовательно,
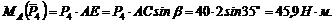
5. Находим момент силы Плечом силы относительно точки А является отрезок АС, так как сила направлена к АС перпендикулярно. Величина момента отрицательная:
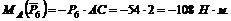
Решение 2 – определение моментов сил относительно точки В (рис. 26, б).
1. Центр моментов в точке В.
2. Через точку В проходят линии действия двух сил: и . Следовательно,
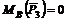и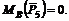 
3. Находим момент силы Плечо силы :
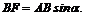
Величина момента отрицательная:
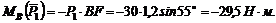
4. Находим момент силы Плечо силы :
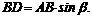
Момент отрицательный:
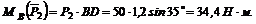
5. Находим момент силы Плечо силы :
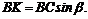
Величина момента положительная:
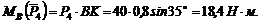
6. Находим момент силы Плечом силы является отрезок ВС. Момент положительный:
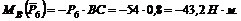
Решение 3 – определение моментов сил относительно точки С (рис. 26, в) рекомендуется выполнить самостоятельно.
Ответ: ; ; ; ; ;
В некоторых задачах силы расположены так, что либо их плечи определяются очень просто – как катеты прямоугольных треугольников, в которых даны гипотенузы, либо плечи заданы в условии задачи (ВС и АС).
Но иногда некоторые силы заданной системы оказываются расположенными относительно выбранного центра моментов так, что определить длину плеча трудно и требуется, например, предварительно вычислить длины еще одного-двух отрезков. В таких случаях целесообразно силу разложить на две составляющие и применить для определения ее момента теорему Вариньона.
Задача 15. Определить моменты относительно точки А сил P1 = 40 H; P2 = 60 H; Р3 = 030 H и Р4 = 50 H, приложенных в точках A, В и С, как показано на рис. 27, а. Углы a = 30°, b = 50°, АB = 2,5 м; ВС = 1,5 м.
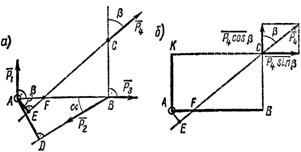
Рис. 27
Решение.
1. Относительно точки А моменты сил , и определяются по выражениям (рис. 27, а):
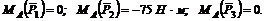
2. Находим момент силы 
Вариант 1-й (рис. 27, а). Плечо АЕ силы 
в данном случае определяем из D AEF, в котором известен только Ð EAF = b. Значит, нужно предварительно определить одну из сторон. Найдем AF:
AF = AB — FB.
Величину FB находим из D CBF, в котором Ð BCF =b:
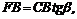
следовательно,
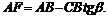
И теперь можем определить плечо АЕ:
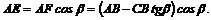
Раскрываем скобки и заменяем 
:
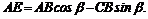
Момент положительный, следовательно:
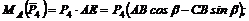
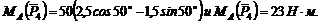
Вариант 2-й. Чтобы избежать определения плеча АЕ, которое в данном случае находится после предварительного вычисления двух отрезков (FB и AF), необходимо момент силы относительно точки А найти по теореме Вариньона: момент равнодействующей плоской системы сил относительно любой точки, лежащей в той же плоскости, равен алгебраической сумме моментов составляющих сил относительно той же точки.
Разложим силу на две составляющие: одну, направленную вдоль отрезка ВС, и другую – перпендикулярно к нему (рис. 29, б).
Модуль первой составляющей P4 cosb, а ее плечо – отрезок АВ, длина которого задана. Модуль второй составляющей P4 sinb, а ее плечо АК = ВС = 1,5 м.
Применяя теорему Вариньона, получаем
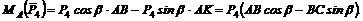
Как видно, получено точно такое же значение момента, что и в первом варианте решения:
§ 7. Приведение системы сил
к данной точке
Если линии действия сил, приложенных к телу, расположены как угодно на плоскости, то их неудобно складывать непосредственно. Целесообразно сначала упростить систему, т. е. заменить ее более простой эквивалентной системой. Такая замена называется приведением системы к данной точке. Эту точку принято называть центром приведения.
Предварительно докажем теорему о параллельном переносе силы: Силу, приложенную к твердому телу в данной точке, можно перенести параллельно в любую другую точку тела, присоединяя при этом пару. Момент присоединенной пары равен моменту данной силы относительно точки, в которую эту силу перенесли (привели).
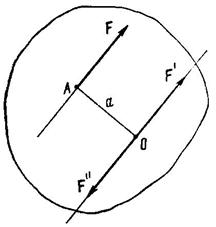
Рис. 28
Доказательство: Пусть сила F приложена к телу в точке А (рис. 28). Приложим в центре О две равные и противоположно направленные силы: F' и F". Согласно 2-й аксиоме при этом механическое состояние тела не изменится. Пусть модули всех сил равны: F = F' = F". Тогда полученную систему из трех сил можно представить как пару (F, F") и силу F', которую можно рассматривать как перенесенную из точки А в точку О силу F. Нетрудно убедиться, что момент пары (F, F")
|
Из за большого объема этот материал размещен на нескольких страницах:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 |
