4. Для того чтобы определить полное ускорение автомобиля в середине А участка 0В, нужно сначала найти скорость vA – скорость автомобиля в момент прохождения им точки А.
Эту скорость найдем, приняв S0 = 0 и S = S0A = 200 м:
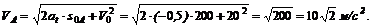
5. Находим нормальное ускорение автомобиля в точке А:
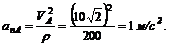
6. И, наконец, находим полное ускорение автомобиля:
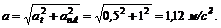
7. Вектор полного ускорения направлен к вектору скорости под углом 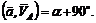 Угол a можно найти при помощи его синуса:
Угол a можно найти при помощи его синуса:
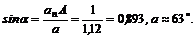
Следовательно,
угол 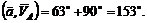
§ 17. Ускорение точки
Как уже указывалось, при неравномерном движении скорость точки непрерывно изменяется с течением времени. При различных видах движения это изменение происходит по-разному. Направление вектора скорости при этом может оставаться постоянным или изменяться.
Векторную величину, характеризующую быстроту изменения модуля и направления скорости, называют ускорением точки.
1. Рассмотрим сначала, как определяется ускорение точки, совершающей прямолинейное движение.
Пусть в данный момент времени t1 точка имеет скорость V1, а через D t с, т. е. в момент t2 = t1 + D t, скорость ее будет V2. Изменение модуля скорости за данный промежуток времени составит D V = V2 - V1. Отношение изменения модуля скорости ко времени, в течение которого это изменение произошло, называют средним ускорением точки:
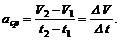
При неограниченном уменьшении промежутка времени (D t ® 0) среднее ускорение будет приближаться к пределу, который представляет собой истинное (мгновенное) ускорение точки. Истинное ускорение
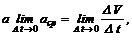 но
но 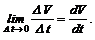 т. е.
т. е.
![]() (26)
(26)
Таким образом, модуль ускорения точки в прямолинейном движении равен первой производной от скорости по времени.
Направление вектора ускорения а совпадает с направлением вектора изменения скорости DV, т. е. при ускоренном движении совпадает с направлением движения, а при замедленном – противоположно ему.
2. Рассмотрим теперь движение точки по криволинейной траектории. Пусть за время D t точка переместится из положения М1 (рис. 67) в положение М2 и скорость ее при этом изменится от V1 до V2. Из рис. 67 видно, что скорость ее при этом изменяется как по величине, так и по направлению. Геометрическую разность скоростей найдем, построив векторы V1 и V2 из одной точки М1 и параллелограмма М2КСЕ. Очевидно, что вектор M1E = DV есть геометрическая разность скоростей V2 и V1, т. е. D V = V2 – V1.
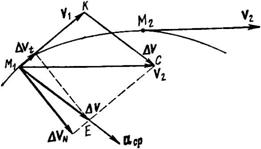
Рис. 67
Поделив вектор изменения скорости D V на промежуток времени D t, получим вектор среднего ускорения ![]() Если предположить, что промежуток времени D t безгранично мал, то можно считать, что вектор аср совпадет с вектором мгновенного ускорения а. Важно отметить, что в данном случае направление ускорения не совпадает с направлением вектора скорости точки, как в случае прямолинейного движения, а совпадает с направлением вектора изменения скорости DV.
Если предположить, что промежуток времени D t безгранично мал, то можно считать, что вектор аср совпадет с вектором мгновенного ускорения а. Важно отметить, что в данном случае направление ускорения не совпадает с направлением вектора скорости точки, как в случае прямолинейного движения, а совпадает с направлением вектора изменения скорости DV.
Разложим вектор DV на две составляющие, одну из которых DVt направим по скорости Vl, т. е. по касательной к траектории в точке M1, а другую DVN перпендикулярно к скорости V1, т. е. по нормали к траектории в данной точке.
Очевидно, что
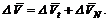
Поделив каждый член последнего уравнения на промежуток времени D t, получим выражение
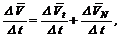
которое согласно определению среднего ускорения можно записать так:
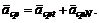
Отсюда следует, что вектор среднего ускорения также можно представить в виде двух составляющих: – аср и aсрN. При неограниченном уменьшении промежутка времени D t в пределе, при D t ® 0, эти составляющие среднего ускорения стремятся к соответствующим составляющим мгновенного ускорения:
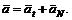 (27)
(27)
Составляющая а направлена по касательной к траектории в данный момент времени и ее называют касательным ускорением.
Касательное ускорение характеризует изменение только модуля скорости и равно первой производной от скорости по времени. Составляющая aN направлена по нормали к траектории в данный момент времени и её называют нормальным ускорением. Оно всегда направлено внутрь вогнутости к траектории к центру кривизны, поэтому его иногда называют центростремительным ускорением.
Нормальное ускорение характеризует изменение направления, скорости точки. Модуль вектора нормального ускорения равен отношению квадрата скорости к радиусу кривизны траектории:
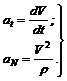 (28)
(28)
Полное ускорение точки в каждый момент времени является геометрической суммой касательного и нормального ускорений.
На рис. 68 показаны направления полного, нормального и касательного ускорения в случаях ускоренного (рис. 68, а) и замедленного (рис. 68, б) движения. Нетрудно установить соотношения между величинами ускорений:
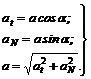 (29)
(29)
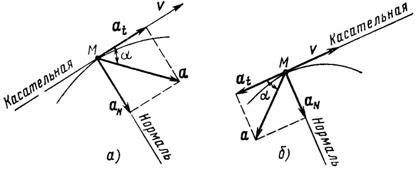
Рис. 68
Криволинейное неравномерное движение точки, при котором полное ускорение представляет собой геометрическую сумму касательного и нормального ускорений, является общим случаем движения. Рассмотрим некоторые частные случаи.
Прямолинейное неравномерное движение. Радиус кривизны прямой r = ¥, значит, ![]() Полное ускорение точки
Полное ускорение точки
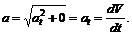
Криволинейное равномерное движение. В этом случае модуль скорости V = const, значит, at = dV/dt = 0. Полное ускорение точки 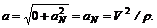 При равномерном движении по кривой точка всегда обладает лишь нормальным ускорением.
При равномерном движении по кривой точка всегда обладает лишь нормальным ускорением.
Прямолинейное равномерное движение. В этом случае r = ¥, V = const, значит,
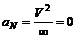 и
и 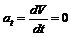
и полное ускорение a = 0.
Задача 39. Точка движется равномерно замедленно по дуге окружности радиусом 80 м в течение 20 с. Определить полное ускорение точки в начале и конце движения, если начальная скорость V0 = 15 м/с, а конечная скорость V = 10 м/с.
Решение
1. Определим постоянное касательное ускорение точки
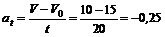 м/с2,
м/с2,
где знак «минус» указывает, что направление ускорения противоположно направлению скорости, т. е. движение является замедленным.
2. Определим нормальное ускорение точки в начальный момент времени:
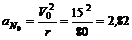 м/с2.
м/с2.
3. Определим нормальное ускорение в конце движения:
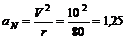 м/с2.
м/с2.
4. Определим полное ускорение точки в начале и конце движения:
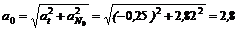 м/с2;
м/с2;
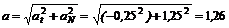 м/с2.
м/с2.
Задача 40. Тело свободно падает на Землю без начальной скорости с высоты Н = 100 м. Пренебрегая сопротивлением воздуха, определить модуль скорости тела в момент падения на Землю.
Решение.
Так как движение тела прямолинейное и равномерно ускоренное, то a = at = g = 9,81 м/с2. Учитывая, что V0 = 0 и s = H, найдем
![]() и
и 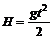 ,
,
откуда
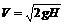 .
.
Подставив значения g и H, имеем 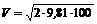 = 44,3 м/с.
= 44,3 м/с.
§ 18. Вращательное движение тела вокруг неподвижной оси
Движение тела, при котором не менее двух каких-либо его точек остаются неподвижными, называется вращательным. Прямая, проходящая через две неподвижные точки, называется осью вращения. Каждая точка тела, не лежащая на оси вращения, описывает окружность, плоскость которой перпендикулярна к оси вращения, а центр лежит на этой оси.

|
Из за большого объема этот материал размещен на нескольких страницах:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 |




