Положение мгновенного центра скоростей непрерывно изменяется с течением времени.
Таким образом, сложное плоскопараллельное движение тела можно упростить, представив его в виде последовательного ряда мгновенных вращений вокруг центров (осей), занимающих различные положения.
Если, например, в данный момент времени МЦС находится в точке С (рис. 86), то скорости любых других точек А и В будут перпендикулярны к прямым, соединяющим эти точки с точкой С, и направлены в сторону вращения, а их модули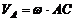 
и 
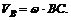
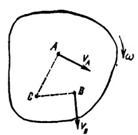
Рис. 86
Зная положение мгновенного центра скоростей и угловую скорость вращения плоской фигуры, можно найти скорость любой точки тела.
Если известны скорости двух произвольных точек фигуры (например vА и vВ), то мгновенный центр скоростей находится в точке пересечения перпендикуляров, восстановленных к этим векторам. Иногда мгновенный центр скоростей С может располагаться и вне фигуры, но в ее плоскости (рис. 87).
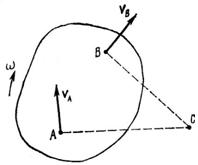
Рис. 87
Модули мгновенных скоростей различных точек фигуры пропорциональны расстояниям от этих точек до мгновенного центра скоростей.
Действительно,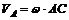 
; 
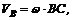отсюда
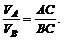
Если же векторы скоростей двух точек фигуры в данный момент времени параллельны другу к другу, то возможны следующие случаи.
1. Векторы скоростей двух точек не перпендикулярны прямой АВ, соединяющей эти точки (рис. 88, а). Перпендикуляры к векторам VA и VB параллельны. Это значит, что МЦС находится в бесконечности, т. е. нет вращения – фигура движется поступательно и VA = VB.
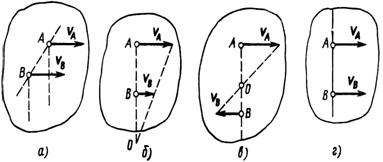
Рис. 88
2. Векторы скоростей точек А и В перпендикулярны к прямой АВ, соединяющей эти точки. Для определения положения МЦС нужно соединить прямой линией концы векторов и найти точку С пересечения этой линии с прямой АВ (рис. 88, б и в). Очевидно, что в этих случаях также справедливо равенство отношений VA/VB = AC/ВС.
3. В случае, изображённом на рис. 88, г (VA = VB), находится в бесконечности – фигура движется поступательно.
Если плоская фигура движется так, что ограничивающий её контур катится без скольжения по некоторой неподвижной кривой, то мгновенный центр скоростей С находится в точке касания контура и неподвижной кривой (рис. 89).
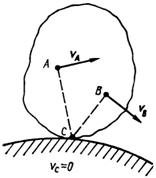
Рис. 89
Задача 55. В четырехзвенном механизме ОАВС (рис. 90) точка А движется по круговой траектории радиусом ОА = 0,15 м, а точка В – по дуге радиусом BС = 0,3 м, ОС = 0,5 м. Определить для данного положения механизма скорость точки В, если vA = 4,55 м/с.
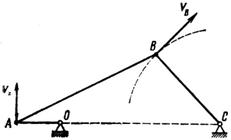
Рис. 90
Решение.
Скорость точки А шатуна, общей с кривошипом ОА, направлена перпендикулярно к радиусу вращения АО, в то время как скорость точки В шатуна, общей со звеном ВС, направлена перпендикулярно радиусу вращения ВС.
Таким образом, направления скоростей двух точек шатуна АВ, совершающего плоское движение, известны. На пересечении перпендикуляров к векторам VA и VB находится МЦС, который совпадает с точкой С.
Так как модули скоростей различных точек фигуры пропорциональны расстояниям, то можно написать
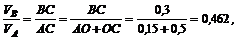
откуда vB = vA - 0,462 = 4,55 - 0,462 = 2,1 м/с.
Задача 56. Кривошип ОА = r = 40 см кривошипно-шатунного механизма (рис. 91, а) вращается с угловой скоростью w = 25 рад/с. Длина шатуна, приводящего ползун В в возвратно-поступательное движение вдоль горизонтальных направляющих, равна АВ = l = 100 см. Определить скорость ползуна В в тот момент, когда кривошип ОА образует с горизонталью угол a = 30°.
Решение 1 – при помощи мгновенного центра скоростей (решение путем сложения переносной и относительной скоростей рекомендуется выполнить самостоятельно).
1.Изобразим на рис. 91, б расчетную схему. Схематично покажем кривошип ОА и шатун АВ в заданном положении. Ползун В, двигающийся поступательно, можно отождествить с точкой В.
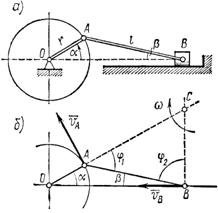
Рис. 91
2. Замечаем, что кривошип совершает вращательное движение, ползун В движется поступательно, а шатун АВ совершает плоскопараллельное движение.
3. Скорость точки А направлена перпендикулярно к кривошипу ОА (по касательной к окружности, которую описывает точка А). Ее числовое значение
Скорость точки В направлена вдоль прямой ВО.
Проведем из точек А и В прямые, перпендикулярные к направлениям скоростей и Найдем в точке их пересечения С мгновенный центр скоростей шатуна.
4. Найдя положение мгновенного центра скоростей, получим
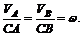
Отсюда
но предварительно нужно узнать значение отношения 
которое, как легко заметить, равно отношению синусов противолежащих углов (теорема синусов):
.
5. Чтобы определить величину этого отношения, необходимо определить углы j1 и j2.
Замечая, что (см. рис. 87, б) j2 = 90° - b, найдем угол b, применив теорему синусов к D OBA:
откуда
Следовательно,
Из того же рис. 91, б видно, что угол j1 является одним из внешних углов D ОBА, поэтому
6. Теперь можно определить числовое значение скорости ползуна В:
Решение 2 – графическим методом.
1. Построим в масштабе m1 = 2,22 см/мм схему кривошипно-шатунного механизма в заданном положении (рис. 92).
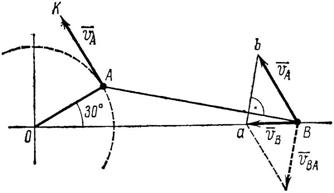
Рис. 92
2. Скорость VA = 10 м/сек точки А изобразим отрезком АК = 18 мм. Значит, масштаб скоростей
3. Из точки В построим вектор (вектор Вb равен вектору и параллелен отрезку AK). Из точки b построим до пересечения с линией ВО (направлением скорости 
) отрезок bа, перпендикулярный к ВА. Получившийся на линии ВО вектор изображает искомую скорость
4. Измерив длину отрезка Ва, найдем, что Ва = 12 мм. Следовательно, числовое значение скоростей точки В
5. Как видно, между результатом, вычисленным при помощи мгновенного центра скоростей (6,75), и результатом, найденным при графическом решении (6,66), имеется расхождение, равное 0,09 (абсолютная ошибка). Следовательно, относительная ошибка, допущенная в графическом решении, составляет
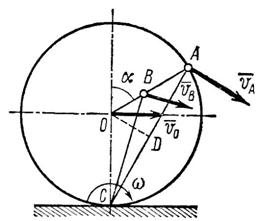
Задача 57. Колесо катится без скольжения по горизонтальной плоскости, причем ось колеса перемещается равномерно со скоростью V0 = 5 м/с. Определить абсолютную скорость точки А на ободе колеса и точки В, находящейся на том же радиусе, в момент, когда радиус колеса, равный ОА = r = 40 см, образует с вертикалью угол a = 60° (рис. 93). Расстояние OB = 15 см.
Решение 1 – при помощи мгновенного центра скоростей.
1. Колесо катится без скольжения, следовательно, точка С соприкосновения колеса с горизонтальной плоскостью является мгновенным центром скоростей, так как абсолютная скорость этой точки VC = 0. Если принять точку С за полюс, то можно считать, что в данный момент колесо совершает вращение вокруг так называемой мгновенной оси, перпендикулярной к плоскости колеса и проходящей через точку С (мгновенный центр скоростей).
2. Определяем угловую скорость колеса:
|
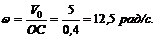
Из за большого объема этот материал размещен на нескольких страницах:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 |
