Рис. 93
3. Определяем абсолютную скорость точки А. Скорость направлена перпендикулярно к прямой АС, соединяющей точку А с мгновенным центром скоростей С,
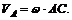
но
Следовательно,
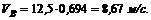
4. Определяем абсолютную скорость точки В. Скорость направлена перпендикулярно к прямой СВ и численно равна
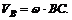
но
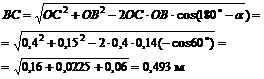
и, следовательно, 
= 12,5×0,493 = 6,17 м/с.
Решение 2 – при помощи сложения переносной и относительной скоростей.
1. Катящееся колесо совершает сложное движение, складывающееся из поступательного движения колеса вместе с осью О (переносного движения) и вращения колеса вокруг оси О (относительного движения).
2. Абсолютная скорость точки А при таком рассмотрении движения колеса равна диагонали параллелограмма ACDE, построенного на переносной и относительной скоростях точки А (рис. 94).
3. Переносная скорость точки А равна скорости оси колеса.
Найдем относительную скорость VАО точки А; VAO = w × AO. Но угловая скорость относительного вращательного движения, как известно, не зависит от выбора полюса, поэтому, приняв за полюс точку С, найдем, что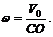 
Следовательно,
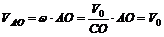(так как СО = АО – радиус колеса).
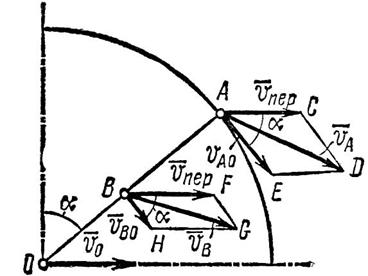
Рис. 94
Таким образом, для точки, расположенной на ободе катящегося без скольжения колеса,
Следовательно, параллелограмм ACDE есть ромб с углом САЕ = a = 60°, поэтому
4. Абсолютная скорость точки В равна диагонали параллелограмма BFGH, построенного на переносной скорости и на относительной скорости , и ее числовое значение можно определить по формуле
Но предварительно необходимо найти скорость VBO, которая определяется из соотношения
Окончательно
Задача 58. Две параллельные рейки (рис. 95, а) движутся в противоположные стороны с постоянными скоростями V1 = 8 м/с и V2 = 2 м/с. Между рейками зажат диск радиусом r = 0,5 м, катящийся по рейкам без скольжения.
Найти угловую скорость диска и скорость его центра.
Решение 1 – при помощи мгновенного центра скоростей.
1. В данном случае известны скорости реек. Но так как диск катится между ними без скольжения, точки А и В в местах соприкосновения диска с рейками имеют те же скорости. Следовательно, и 
(рис 95, б). Как видно, точки А и В лежат на прямой, перпендикулярной к направлениям этих скоростей.
Соединив концы D и Е векторов AD и BE, изображающих скорости и найдем на прямой АВ точку С – мгновенный центр скоростей диска.
2. Скорость иа центра диска определяется по формуле
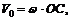
где w – угловая скорость диска.
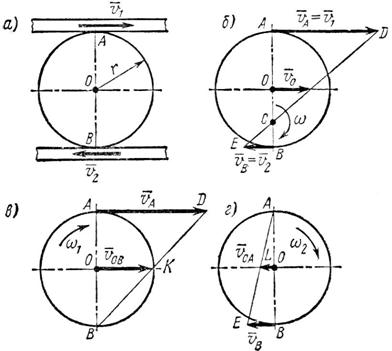
Рис. 95
3. Величины угловой скорости w и расстояния ОС находим из равенств
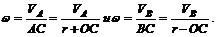
Так как левые части обоих равенств равны между собой, то
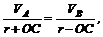
отсюда
и
4. Находим скорость V0:
Решение 2 – методом последовательной остановки реек.
1. Плоское движение диска образуется вследствие независимого друг от друга перемещения реек. Поэтому скорость центра диска можно получить как результат геометрического сложения скоростей, получаемых точкой О от перемещения каждой рейки.
2. Мысленно остановим нижнюю рейку (рис. 95, в). Тогда благодаря передвижению верхней рейки диск будет катиться по нижней без скольжения и в точке В образуется мгновенный центр скоростей.
Соединим точку В с точкой D (концом вектора 
) и получим треугольник BAD, в котором вектор изображает скорость центра диска при неподвижной нижней рейке.
Так как ОК – средняя линия треугольника BAD,
Угловая скорость диска в этом движении
3. Теперь мысленно остановим верхнюю рейку (рис. 95, г). Диск будет катиться без скольжения по верхней рейке, имея мгновенный центр скоростей в точке А.
Соединив точку А с концом Е вектора получим треугольник ABE, определяющий скорость центра диска при неподвижной верхней рейке.
И здесь OL – средняя линия треугольника ABE, поэтому
Угловая скорость диска в этом движении
4. При одновременном движении обеих реек скорость центра диска
так как обе скорости и направлены вдоль одной прямой, но в противоположные стороны.
5. Угловая скорость диска определяется как сумма угловых скоростей w1 и w2, найденных выше:
СОДЕРЖАНИЕ
Глава 1. ПЛОСКАЯ СИСТЕМА СХОДЯЩИХСЯ СИЛ.. 3
§ 1. Сложение двух сходящихся сил. 3
§ 2. Разложение силы на две сходящиеся составляющие. 6
§ 3. Сложение плоской системы сходящихся сил. Силовой многоугольник 11
§ 4. Проекция силы на ось. Проекция силы на две взаимно-перпендикулярные оси координат 20
§ 5. Условия равновесия плоской системы сходящихся сил. 24
Глава 2. ПЛОСКАЯ СИСТЕМА ПРОИЗВОЛЬНО
РАСПОЛОЖЕННЫХ СИЛ.. 26
§ 6. Момент силы относительно точки. 26
§ 7. Приведение системы сил к данной точке. 32
§ 8. Равнодействующая плоской системы сил. Теорема Вариньона
о моменте равнодействующей. 35
§ 9. Уравнения равновесия произвольной плоской системы сил. 40
§ 10. Виды опор балочных систем. 49
Определение опорных реакций. 49
Глава 3. ПРОСТРАНСТВЕННАЯ СИСТЕМА СИЛ.. 55
§ 11. Пространственная система сходящихся сил. 55
§ 12. Момент силы относительно оси. 60
§ 13. Условия равновесия произвольной пространственной
системы сил. 64
Глава 4. КИНЕМАТИКА ТОЧКИ.. 74
§ 14. Основные положения кинематики. 74
§ 15. Способы задания движения точки. 75
§ 16. Скорость точки. 77
§ 17. Ускорение точки. 85
§ 18. Вращательное движение тела вокруг неподвижной оси. 89
§ 19. Частные случаи вращательного движения. 91
Глава 5. СЛОЖНОЕ ДВИЖЕНИЕ ТОЧКИ.. 99
§ 20. Абсолютное движение и его составляющие. 99
§ 21. Сложение скоростей и ускорений точки в сложном
движении. 99
Глава 6. СЛОЖНОЕ ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА.. 110
§ 22. Плоскопараллельное движение тела. 110
§ 23. Определение скорости точки тела при плоскопараллельном движении 112
§ 24. Мгновенный центр скоростей. 114
Учебное издание
ТЕОРЕТИЧЕСКАЯ МЕХАНИКА
Часть 1
Учебное пособие
редактор
Корректор
Компьютерная верстка
Лицензия на издательскую деятельность ИД
Подписано в печать 14.10.2003. Формат 60´84/16.
Бумага типографская. Печать офсетная. Усл. печ. л. 7,44. Уч.-изд. л. 7,2.
Тираж экз. Заказ
_____________________________________________________________
Издательство Владивостокского государственного университета
экономики и сервиса
690600, Владивосток, ул. Гоголя, 41
Отпечатано в типографии ВГУЭС
690600, Владивосток, ул. Державина, 57
|
Из за большого объема этот материал размещен на нескольких страницах:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 |
