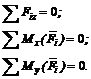 (20)
(20)
Задача 29. Вал ворота и его рукоятка расположены в одной вертикальной плоскости (рис. 54). Груз G = 500 кН, подвешенный на вороте, удерживается в равновесии горизонтальной силой F, приложенной в середине рукоятки перпендикулярно к ней. Пренебрегая весом вала, определим силу F и реакции подшипников А и В.
Решение.
1. Приложим к вороту активные силы F и G.
2. Реакции подшипников разложим на составляющие RAx, RAz, RBx, RBz. Составляющие RAy и RBy отсутствуют, поскольку активные нагрузки действуют в плоскостях, перпендикулярных оси вала, и не могут смещать вал вдоль его оси.
3. Составим уравнения равновесия:
4. После решения уравнений получим: F = 250 кН; RAx = – 350 кН; RAz = 250 кН; RBx = –600 кН; RBz = 250 кН.
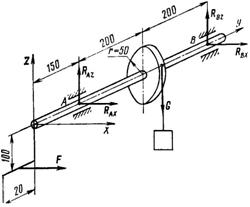
Рис. 54
Задача 30. Квадратная крышка весом 400 H удерживается приоткрытой на 60° над горизонтальной плоскостью противовесом Q (рис. 55). Определить, пренебрегая трением на блоке D, вес противовеса Q и реакции шарниров A и B, если блок D укреплен на одной вертикали с шарниром А и AD = АС.
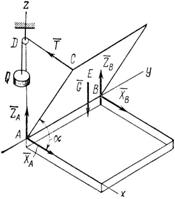
Рис. 55
Решение.
1. Выбрав за начало координат точку А и расположив оси так, как показано на рис. 55, покажем на этом же рисунке активные силы и реакции опор.
На крышку действует сила тяжести ![]() которую считаем приложенной в точке Е (центр симметрии квадрата), и реакция нити CD, приложенная в точке С. Сила Т численно равна весу Q противовеса. Действие этих сил уравновешивается реакциями шарниров А и В. Так как силы и
которую считаем приложенной в точке Е (центр симметрии квадрата), и реакция нити CD, приложенная в точке С. Сила Т численно равна весу Q противовеса. Действие этих сил уравновешивается реакциями шарниров А и В. Так как силы и ![]() действуют в плоскостях, перпендикулярных к оси у, то реакции шарниров лежат в плоскостях, перпендикулярных к той же оси. Поэтому реакцию шарнира А заменим двумя составляющими и , а реакцию шарнира В – составляющими и
действуют в плоскостях, перпендикулярных к оси у, то реакции шарниров лежат в плоскостях, перпендикулярных к той же оси. Поэтому реакцию шарнира А заменим двумя составляющими и , а реакцию шарнира В – составляющими и ![]() .
.
2. Если составление уравнений равновесия по рис. 55 затруднительно, можно предварительно изобразить крышку вместе с действующими на нее силами в трех проекциях, как это сделано на рис. 56:
а) вид спереди, ось х перпендикулярна к плоскости проекции;
б) вид сверху, ось z перпендикулярна к плоскости проекции;
в) вид слева, ось у перпендикулярна к плоскости проекции.
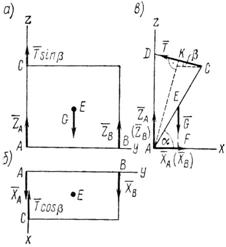
Рис. 56
3. Составим уравнения равновесия.
Для составления уравнений проекций на ось х воспользуемся рис. 56, б или 56, в:
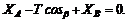 (1)
(1)
На ось у силы не проектируются, так как все они перпендикулярны к этой оси.
Для составления уравнений проекций на ось z воспользуемся рис. 56, а или 56, в:
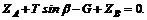 (2)
(2)
Для составления уравнения моментов относительно оси х воспользуемся рис. 56, а:
 (3)
(3)
Для составления уравнения моментов относительно оси у воспользуемся рис. 56, в:
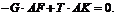 (4)
(4)
Для составления уравнения моментов относительно оси z воспользуемся рис. 56, б:
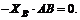 (5)
(5)
4. Решаем полученные уравнения.
Из уравнения (5) находим (так как AB ¹ 0): ХB = 0.
Из уравнения (4)
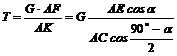 .
.
Так как АЕ = АС / 2, то 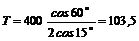 H.
H.
Из уравнения (3)
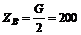 H.
H.
Из уравнения (2)
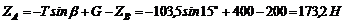
(угол b = 15°, так как треугольник ACD равнобедренный). Из уравнения (1)
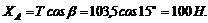
Таким образом, чтобы крышка находилась в равновесии приоткрытой под углом 60°, вес противовеса должен быть Q = Т = 103,5 H. При этом реакция шарнира А имеет две составляющие: горизонтальную ХА = 100 H и вертикальную ZA = 173,2 H, а реакция шарнира В направлена вертикально и равна ZB = 200 H.
Задача 31. На вал 1 ворота намотана веревка, удерживающая груз Q (рис. 57). Радиус колеса 2 ворота в четыре раза больше радиуса вала. Веревка, прикрепленная к ободу колеса и натягиваемая грузом силой Р = 80 H, сходит с колеса в точке F по касательной; радиус DF колеса образует с вертикалью угол a = 60°. Определить величину груза Q, при котором ворот остается в равновесии, а также реакции подшипников А и В, если общий вес вала и колеса G = 600 Н и приложен в точке С (АС=0,4 м).
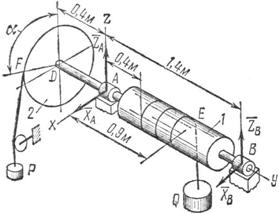
Рис. 57
Решение.
1. Три нагрузки – вес ![]() и грузы и приложенные к вороту, уравновешиваются реакциями подшипников А и В. Нагрузки действуют в плоскостях, перпендикулярных к оси вала, и, следовательно, не смещают вал вдоль оси, поэтому и реакции подшипников расположатся в плоскостях, перпендикулярных к этой же оси. Заменим их составляющими и
и грузы и приложенные к вороту, уравновешиваются реакциями подшипников А и В. Нагрузки действуют в плоскостях, перпендикулярных к оси вала, и, следовательно, не смещают вал вдоль оси, поэтому и реакции подшипников расположатся в плоскостях, перпендикулярных к этой же оси. Заменим их составляющими и ![]() (рис. 57). Следует учесть, что обычный подшипник не создает реакции, направленной вдоль оси вала. Если на вал действуют нагрузки, смещающие вал вдоль оси, то один из подшипников должен быть заменен подпятником.
(рис. 57). Следует учесть, что обычный подшипник не создает реакции, направленной вдоль оси вала. Если на вал действуют нагрузки, смещающие вал вдоль оси, то один из подшипников должен быть заменен подпятником.
2. Изобразим ворот со всеми действующими на него силами в трех проекциях (рис. 58 а, б, в) и при помощи их составим уравнения равновесия.
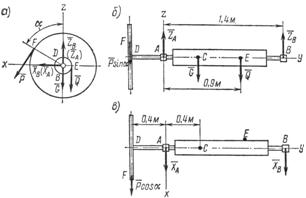
Рис. 58
Так же как и в предыдущей задаче, уравнение проекций на ось у превратится в тождество вида 0 = 0. При составлении уравнения моментов относительно оси у (уравнения (4)) нужно учитывать, что радиус колеса R в четыре раза больше радиуса вала r (R = 4r).
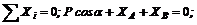 (1)
(1)
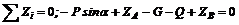 ; (2)
; (2)
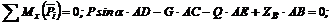 (3)
(3)
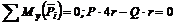 ; (4)
; (4)
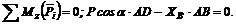 (5)
(5)
3. Из уравнения (5)
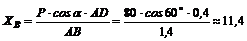 Н.
Н.
Из уравнения (4)
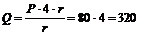 Н.
Н.
Из уравнения (З)
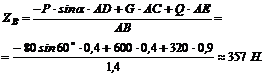
Из уравнения (2)
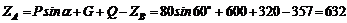 Н.
Н.
Из уравнения (1)
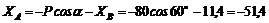 Н.
Н.
Задача 32. На вале редуктора жестко укреплены два зубчатых колеса: коническое 1 и цилиндрическое 2 (рис. 59, а). Левая цапфа вала опирается на подшипник, воспринимающий только радиальную силу давления, действующую перпендикулярно к оси вала, а правая цапфа (пята) опирается на подпятник, т. е. на опору, способную, кроме радиальной силы давления, воспринимать и осевую (силу, действующую вдоль оси вала).
На колесо 1 действуют три силы: касательная P1 = 4 кH (окружное усилие); радиальная Q1 = l,28 кН и осевая S1 = 0,48 кН. Определить в положении равновесия силы Р2 и Q2 = 0,36 P2, приложенные к колесу 2, а также реакции опор А и В. Необходимые размеры (в мм) даны на рис. 55, а. Весом вала и колес пренебречь.
Решение.
1. Заданные и искомые силы, приложенные к колесам 1 и 2, приведем к точкам С1 и С2 на геометрической оси вала (рис. 59, б).
Сила Q1 = l,28 кН, действующая вдоль радиуса колеса, переносится в точку С1 непосредственно. Для приведения к точке C1 силы P1 = 4 кH, приложим к этой точке уравновешенную систему сил ![]() и
и ![]() и тогда, кроме приведенной силы
и тогда, кроме приведенной силы ![]() , образуется пара сил
, образуется пара сил 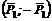 , отмеченная на рисунке одной черточкой (присоединенная пара сил). При переносе в точку С1 силы S1=0,48 кH аналогичным образом появляется пара
, отмеченная на рисунке одной черточкой (присоединенная пара сил). При переносе в точку С1 силы S1=0,48 кH аналогичным образом появляется пара 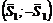 , отмеченная двумя черточками. Сила , действующая вдоль радиуса колеса 2, переносится в точку С2 непосредственно. При переносе в точку С2 силы
, отмеченная двумя черточками. Сила , действующая вдоль радиуса колеса 2, переносится в точку С2 непосредственно. При переносе в точку С2 силы ![]() образуется пара
образуется пара 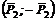 , отмеченная на рисунке тремя черточками.
, отмеченная на рисунке тремя черточками.

|
Из за большого объема этот материал размещен на нескольких страницах:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 |




