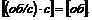
3. Обозначив e' – угловое ускорение, выраженное через обороты, число оборотов можно представить в виде nк = n0 + e't и тогда

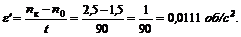
4. Найдем п1 – скорость вращения маховика через t1 = 45 с после начала равноускоренного вращения:

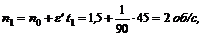
что соответствует

n1 = 2 × 60 = 120 об/мин.

Теперь находим при этой скорости вращения маховика скорость точек на его ободе:

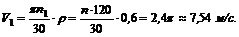
Если же n1 выражено в об/с, то

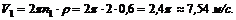
Задача 45. Вал, вращающийся равноускоренно из состояния покоя, в первые 12 с совершает 95,5 оборота. С каким угловым ускорением вращается вал и какую угловую скорость он приоб­ретает?

Решение.

1. Угловое перемещение за время t=12 с равноускоренного движения составляет

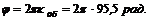
2. Находим угловое ускорение вала:

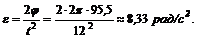
3. К концу 12-й секунды вал приобретает угловую скорость:

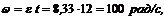
что соответствует

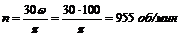
Задача 46. Колесо, вращающееся с частотой 1500 об/мин, при торможении начинает вращаться равнозамедленно и через 30 с останавливается. Определить угловое ускорение и число оборотов колеса с момента начала торможения до остановки.

Решение.

1. Выразим начальную угловую скорость в рад/с:

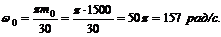
Найдем угловое ускорение:

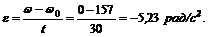
2. Определим число оборотов в виде

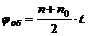
Тогда число оборотов вала за t = 30 с = 0,5 мин

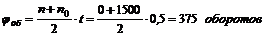
Задача 47. Вращение вала в течение первых 20с проис­ходит согласно уравнению j = 0,8t3.

Определить угловую скорость вала в конце 20-й секунды; угло­вое ускорение в начале движения, в конце 10-й и 20-й секунд; сколько всего оборотов делает вал за 20 с.

Решение.

1. Определим число оборотов вала за 20с. Для этого пред­варительно найдем угол поворота за t = 20 с:

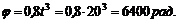
И теперь

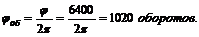
2. Определим уравнение угловой скорости вала:

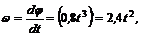
3. Найдем угловую скорость вала в конце 20-й секунды (t = 20 с):

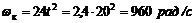
Если выразить эту угловую скорость в об/мин, то

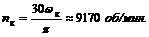
4. Определим уравнение углового ускорения:

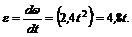
5. Найдем угловое ускорение в начале движения (t0=0), в конце 10- й (t1= 10 с) и 20-й секунд (t2 = 20 с):

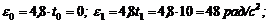
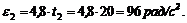
Глава 5. СЛОЖНОЕ ДВИЖЕНИЕ ТОЧКИ

§ 20. Абсолютное движение и его составляющие

В предыдущих главах мы рассматривали движение точки и тела относительно системы отсчета, связанной с Землей, которую условно считали неподвижной. Движение относительно этой «неподвижной» системы координат принято называть абсо­лютным. Но иногда приходится рассматривать движение точки относительно системы, связанной с телом, которое само движется относительно Земли или тел, неподвижно скрепленных с ней (стены здания, рельсы, машины и т. п.). В этом случае абсолютное движение точки удобно представить себе как сложное движение, состоящее из двух (или более) независимых движений.

Движение точки относительно подвижной системы отсчета называют относительным, а движение точки вместе с подвижной системой отсчета относительно неподвижной системы отсчета называют переносным.

Для примера рассмотрим движение поднимаемого при помощи крана груза в условиях, когда стрела крана одновременно пово­рачивается вокруг своей оси. Движущейся системой отсчета в этом случае является стрела крана. Относительно нее груз движется прямолинейно вверх – это относительное движение. Одновремен­но вместе со стрелой груз совершает движение по дуге окружно­сти относительно «неподвижной» Земли – это переносное движе­ние груза.

Наблюдатель, стоящий на Земле, видит абсолютное движение груза, складывающееся из двух происходящих одновременно дви­жений.

Сложным также является движение человека по движущейся лестнице эскалатора: движение человека по отношению к ступеням является относительным, а перемещение его вместе со ступенями относительно неподвижных стен тоннеля является переносным. Абсолютным будет движение человека относительно неподвижных стен.

Таким образом, абсолютное движение точки – совокупность двух движений: относительного и переносного. При этом разли­чают абсолютную, относительную и переносную траектории и соответственно такие же скорости и ускорения точки.

§21. Сложение скоростей и ускорений точки
в сложном движении

В ряде случаев по заданным относительному и переносному движениям определяют абсолютное движение точки. Иногда зада­ны абсолютное и одно из составляющих движений, а необходимо определить другое составляющее движение.

Рассмотрим, как определяют абсолютное движение точки (т. е. абсолютные перемещения, скорость и ускорение), если ее отно­сительное и переносное движения прямолинейны и направлены под углом друг к другу. Пусть груз М движется вниз по наклонной плоскости и за промежуток времени D t перемещается относительно нее на D Sотн (рис. 72).

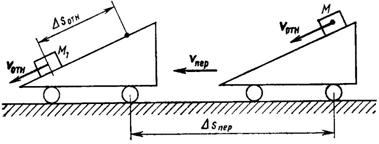
Рис. 72

Наклонная плоскость за этот же промежу­ток времени D t движется прямолинейно относительно Земли, и груз вместе с ней совершает переносное перемещение D Sпер. Изобразим эти перемещения в виде вектора D Sотн и D Sпер, на­правление которых совпадает с направлениями соответствующих движений. Диагональ параллелограмма, построенного на этих векторах (рис. 73), будет абсолютным перемещением груза из точки М в точку M1. При этом, если переносное и относительное перемещения прямолинейны, абсолютное перемещение

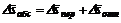. (37)

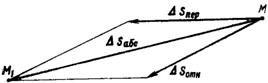
Рис. 73

Поделим каждый член уравнения (37) на время D t, в течение которого происходило движение, и устремляя D t ® 0, получим выражение:

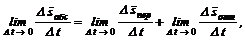
где каждый член представляет собой в пределе соответствующую мгновенную скорость груза, т. е.

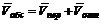. (38)

Следовательно, в случае, если относительное и переносное движения прямолинейны, абсолютная скорость точки в каждый момент времени определяется как геометрическая сумма относи­тельной и переносной скоростей. Графически абсолютная скорость точки может быть определена по правилу параллелограмма или треугольника (рис. 74, а и б).

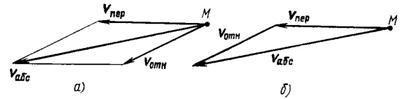
Рис. 74

Для определения модуля абсолютной скорости можно исполь­зовать теорему косинусов:

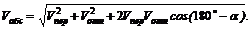
Учитывая, что 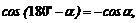имеем

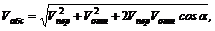
где a – угол между направлениями относительной и переносной скоростей.

Из последнего выражения следует, что: 1) при a = 0°, когда направления относительной и переносной скоростей совпадают,

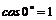и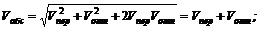

2) при a = 180°, когда относительное и переносное движения прямо противоположны, cos 180° = – 1 и

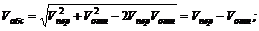
3) при a = 90°, cos 90° = 0 и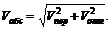

Аналогичные рассуждения позволяют написать выражение для ускорений:

которое, однако, справедливо лишь для случая, когда переносное движение является поступательным.

Следует заметить, что выражения (37) и (38) справедливы и в общем случае, когда переносное и относительное движения криволинейны, так как криволинейное движение можно рас­смотреть как совокупность бесконечно малых прямолинейных перемещений, направленных вдоль соответствующих скоростей.

Задача 48. В кулисном механизме (рис. 75, а) кулиса ОС качается вокруг оси 0, перпендикулярной плоскости чертежа. Ползун А перемещается вдоль кривошипа и приводит в возвратно-поступательное движение стержень АВ, который перемещается в вертикальных направляющих К. Определить скорость движения ползуна относительно кулисы ОС, если ОК = l, а угловая скорость кривошипа w.

Из за большого объема этот материал размещен на нескольких страницах: 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20