Определить, за какое время каждый из них проедет расстояние 100 км. Через сколько часов и где они встретятся?
Решение.
1. Находим время, затраченное первым велосипедистом на проезд от точки A до В:
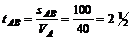ч.
2. Находим время, затраченное вторым велосипедистом на проезд от точки В до А:
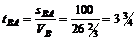ч.
3. Время и место встречи велосипедистов наиболее просто определить графически. Расстояние между пунктами А и В, равное 100 км, изобразим на оси ординат отрезком в 50 мм (рис. 63), т. е. в масштабе ms= 2 км/мм
.
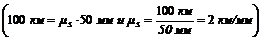По оси абсцисс отложим время в масштабе mt = 0,1 ч/мм (4 часа изображены отрезком 40 мм, поэтому 4 ч = m × 40 мм и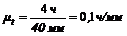 
).
Первый велосипедист расстояние от А до В проезжает за 2,5 ч. Его перемещение изображается на графике прямой ОВ1.
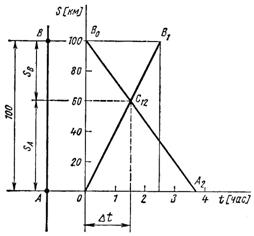
Рис. 63
Второй велосипедист расстояние от B до A проезжает за 33/4 ч и его перемещение изображается на графике прямой В0А2.
Точка С12 пересечения обоих графиков указывает место и время встречи. Встреча происходит на расстоянии SA = 60 км от пункта А (или на расстоянии SB = 40 км от пункта В) через D t = 1,5 ч после начала движения велосипедистов.
Если вместо графического решения применить аналитическое, то нужно рассуждать таким образом.
Допустим, что место встречи происходит на расстоянии s от пункта А, а время встречи D t, считая от начала движения. Тогда уравнение движения первого велосипедиста примет вид
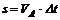(1)
и уравнение движения второго велосипедиста
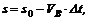
где s0 = 100 км – расстояние второго велосипедиста от пункта А в момент начала отсчета (при t = 0).
Так как левые части уравнения (1) и (2) равны, то
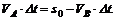
Отсюда
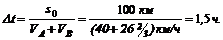
Из уравнения (1) определяем S:
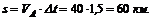
Задача 34. Определить, с какими скоростями движутся точки А, В и С, расположенные на концах секундной, минутной и часовой стрелок часов. Принять длину секундной и минутной стрелок, равную 14 мм, и длину часовой стрелки – 10 мм (рис. 64).
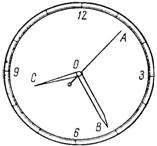
Рис. 64
Решение.
1. Скорости данных точек найдем из формулы
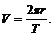
2. Определим исходные данные.
Для точки А (конец секундной стрелки)
ОА = тA = 14 мм; ТА = 1 мин = 60 с.
Для точки В (конец минутной стрелки)
0В = rB = 14 мм; ТB = 1 ч = 3600 с.
Для точки С (конец часовой стрелки)
ОС = rC = 10 мм; ТC = 12ч = 43 200 с.
3. Находим искомые скорости:
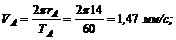
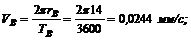
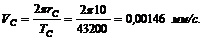
Неравномерное движение точки. При неравномерном движении скорость точки непрерывно изменяется с течением времени, т. е. V = f(t).
Пусть точка, закон движения которой задан функцией s = f(t), движется из положения М0 (рис. 65) в положение М1 неравномерно в течение промежутка времени t = t1 – t0. Тогда отношение 
представляет собой среднюю скорость движения за данный промежуток времени. Но средняя скорость не дает представления о быстроте движения в каждый момент времени. Поэтому, кроме средней приходится определять мгновенную скорость, или скорость в данный момент.
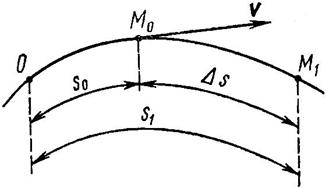
Рис. 65
Чем меньше промежуток времени D t, тем ближе средняя скорость приближается к мгновенной. В пределе, когда D t®0, – средняя скорость примет значение истинной скорости в данный момент времени:
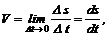(25)
т. е. модуль мгновенной скорости равен первой производной от пути по времени. Вектор скорости точки направлен по касательной к траектории движения в данной точке и направлен в сторону движения.
В частном случае, если траектория движения представляет собой прямую линию, вектор скорости направлен вдоль этой прямой в сторону движения. Модуль мгновенной скорости в этом случае определяется так же: 
Задача 35. Точка обода маховика движется по закону S = 1,5t2, где s – в м, t – в с. Определить скорость точки в момент времени t = 10 с и среднюю скорость за 10 с.
Решение.
1. Мгновенную скорость точки при t = 10 с найдем, продифференцировав уравнение движения:
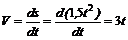м/с,
откуда для t = 10 с V = 30 м/с.
2. Среднюю скорость найдем по формуле
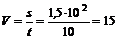м/с.
Задача 36. Шарик, размерами которого можно пренебречь, начинает скатываться по наклонной плоскости из состояния покоя. Через 20 с после начала движения шарик находится от исходного положения на расстоянии 6 м.
Определить ускорение шарика и его скорость в конце 10-й и 20-й с, а также расстояние, пройденное шариком за первые 10 с.
Решение.
1. Из условия задачи следует, что S0 = 0 и V0= 0. Пройденное за t2 = 20 с расстояние S20 = 6 м. Даны четыре величины. Требуется определить ускорение шарика (движение прямолинейное, значит определить нужно только at), скорости V10, V20 и расстояние s10.
2. Найдем скорость шарика, которую он приобретает в конце 20-й с:
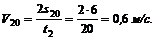
3. Найдем ускорение шарика, которое он имеет, двигаясь по наклонной плоскости:
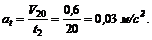
4. Теперь можно найти скорость в конце 10-й с (t1 = 10 с):
V10 = a1 × t1 = 0,03×10 = 0,3 м/с.
5. Находим расстояние, пройденное точкой за первые 10 с:
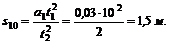
Задачу можно решить в ином порядке. Сначала определить ускорение
Затем определить V10 и V20 и, наконец, найти s10.
Задача 37. Автомобиль, движущийся равномерно и прямолинейно co скоростью 60 км/ч, увеличивает в течение 20 с скорость до 90 км/ч. Определить, какое ускорение получит автомобиль и какое расстояние он проедет за это время, считая движение равноускоренным.
Решение.
1. Здесь также четыре данных величины:
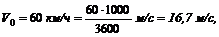
V20 = 90 км/ч = 25 м/с, t0-20 = 20 с и s0 = 0,
так как движение автомобиля рассматривается только на том участке траектории (дороги), где он движется с ускорением.
2. Полагая, что в начальный момент времени S0= 0, найдем S0-20:
м.
3. Из формулы (2) найдем ускорение, полученное автомобилем:
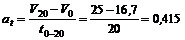м/с2.
Задача 38. Имея скорость 20 м/с, автомобиль въезжает на криволинейный участок дороги, имеющий радиус закругления 200 м.
За 40 с равнопеременного движения он проезжает расстояние 400 м.
Определить, с каким касательным ускорением движется автомобиль, какова его скорость в конце пройденных 400 м и каково полное ускорение на середине этого пути.
Решение.
1. Изобразим участок дороги, по которой движется автомобиль (рис. 66): О – начало участка, В – конец участка и А – его середина.
Для равнопеременного движения в задаче имеется четыре основных данных: S0 = 0 (так как за начало отсчета движения принимаем точку О); V0 = 20 м/с; t0B = 40 с и S0B = 400 м; кроме того, известен радиус закругления 01A = r = 200 м.
2. Найдем скорость vB в конце участка дороги длиной S0B = 400 м (полагая, что S0 = 0):
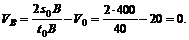
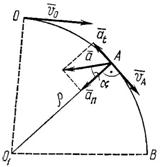
Рис. 66
В конце рассматриваемого участка автомобиль останавливается, значит, движение равнозамедленное.
3. Найдем касательное ускорение автомобиля:
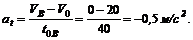
Получившееся отрицательное значение ускорения – подтверждение того, что движение автомобиля равнозамедленное.
|
Из за большого объема этот материал размещен на нескольких страницах:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 |
