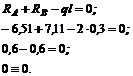
Полученное тождество указывает на правильность решения.
Задача 24. Определить реакцию жесткой заделки и опорный момент для балки, нагруженной, как указано на рис. 44. В заделке возникают вертикальная реакция RA и опорный момент MR. Горизонтальная составляющая отсутствует, так как нет сил, стремящихся сдвинуть балку в горизонтальном направлении.
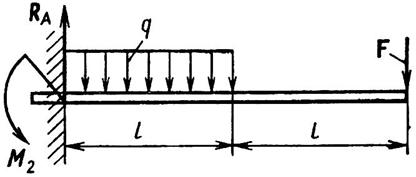
Рис. 44
Решение.
Для решения задачи составим два уравнения равновесия:
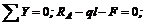
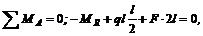
откуда 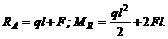
Задача 25. На консольную балку, имеющую в точке А шарнирно-неподвижную, а в точке В шарнирно-подвижную опору, действуют две нагрузки (рис. 45, а): в точке D – сосредоточенная нагрузка P = 8 кН, а на участке СВ – равномерно распределенная нагрузка, интенсивностью q=2 кН/м. Определить реакции опор.
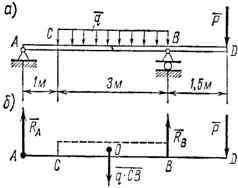
Рис. 45
Решение.
1. В этой задаче, кроме сосредоточенной силы Р, на участке СВ действует равномерно распределенная сила, интенсивность которой q. Полная величина этой нагрузки (ее равнодействующая) равна q × CB и приложена в точке О посредине участка СВ (рис. 45, б), т. е.
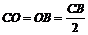 .
.
Реакция подвижного шарнира направлена вертикально (перпендикулярно к опорной поверхности). Следовательно, и реакция неподвижного шарнира направлена вертикально. Таким образом, на балку действует система параллельных сил ( рис. 45, б).
3. Составим два уравнения моментов относительно точек В и А:
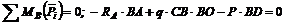 ; (1)
; (1)
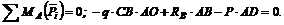 (2)
(2)
4. Из уравнения (1)
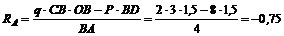 кН.
кН.
Отрицательное значение реакции RA означает, что она направлена вниз, а не вверх, как показано на рис. 45, б, потому что момент силы Р относительно опоры В больше, чем момент равномерно распределенной нагрузки.
Из уравнения (2) находим RB:
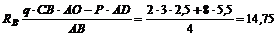 кН.
кН.
Таким образом, реакция шарнира А равна RA = 0,75 кH и направлена вертикально вниз; реакция шарнира В составляет Rв = 14,25 кH и направлена вертикально вверх.
5. Для проверки решения можно использовать уравнение проекций на вертикальную ось.
Глава 3. ПРОСТРАНСТВЕННАЯ СИСТЕМА СИЛ
§ 11. Пространственная система
сходящихся сил
Плоская система сил, которую мы рассматривали до сих пор, является частным случаем общей пространственной системы сил. На практике в большинстве случаев встречаются пространственные системы сил, которые можно разложить на несколько плоских систем. Но бывают случаи, когда этого сделать нельзя, и тогда нужно рассматривать пространственную систему. Простейшей пространственной системой является система, состоящая из трех сил, приложенных в одной точке.
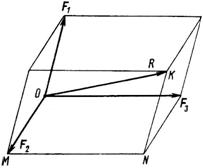
Рис. 46
Пусть дана система из трех сил: F1, F2, F3, приложенная в точке О (рис. 46). Чтобы найти равнодействующую системы, построим пространственный силовой многоугольник OMNK. Замыкающая стороны этого многоугольника ОK по модулю и направлению равна равнодействующей данной системы:
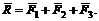
Если достроить многоугольник до параллелепипеда, как указано на рис. 43, то увидим, что равнодействующая R является его диагональю, а силы F1, F2 и F3 – его сторонами.
Следовательно, равнодействующая трех сил, приложенных в одной точке и не лежащих в одной плоскости, по модулю и направлению равна диагонали параллелепипеда, построенного на данных силах.
Если равнодействующая система сходящихся сил равна нулю R = 0, то силы находятся в равновесии и силовой многоугольник замкнут.
Пусть сила R есть равнодействующая пространственного пучка сил F1, F2, F3, …,Fn. Разложим силу R согласно правилу параллелепипеда на три составляющие: Rx, Ry, и Rz, направленные по трем взаимно перпендикулярным осям (рис. 47). Рассматривая силу R как равнодействующую трех составляющих: Rx, Ry и Rz, отметим, что она представляет собой диагональ прямоугольного параллелепипеда и ее модуль:
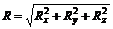 , (15)
, (15)
где Rx, Ry, и Rz — проекции вектора R на координатные оси.
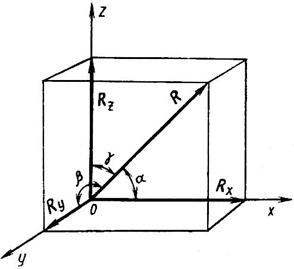
Рис. 47
Направление равнодействующей определяется косинусами углов между силой R и осями координат:
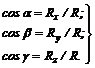 (16)
(16)
Согласно теореме о проекции равнодействующей на ось имеем
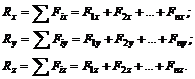
Если система сходящихся сил находится в равновесии, то
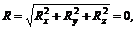
значит,
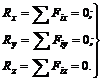 (17)
(17)
Уравнения (17) выражают условия равновесия пространственной системы сходящихся сил; из них следует, что пространственная система сходящихся сил находится в равновесии, если алгебраические суммы проекций составляющих сил на три взаимно перпендикулярные оси равны нулю.
Задача 26. Найти усилия в стержне АВ (рис. 48) и цепях АС и AD, поддерживающих груз G = 10 кН, если a = 60°, b = 30°, g = 45°. ACED – прямоугольник, лежащий в горизонтальной плоскости. Крепление в точке В шарнирное.
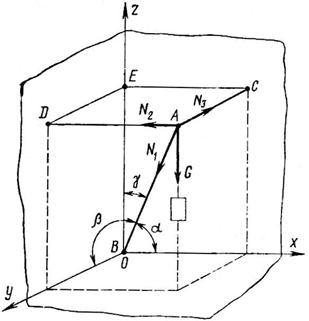
Рис. 48
Решение.
Освободившись от связей и заменив их реакциями, имеем в точке А систему сходящихся сил (N1, N2, N3 и G). Выбрав направление координатных осей, составляем уравнения равновесия:
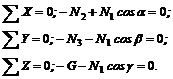
Решая уравнения, получим:
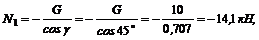
где знак «минус» указывает на то, что стержень АВ сжат, а не растянут, как мы вначале предположили:
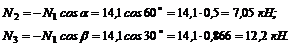
Задача 27. Переносный кран, поднимающий груз массой m = 2000 кг, устроен так, как указано на рис. 45, a; AB = AD = AE = 2 м; угол DAE = 120°, плоскость ABC, в которой расположена стрела АС крана, делит двугранный угол DAE пополам. Определить силу, сжимающую вертикальную стойку АВ, и силы, растягивающие тросы BD и BF; весом частей крана пренебречь.
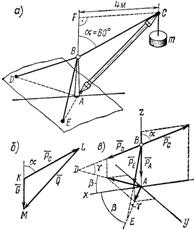
Рис. 49
Решение.
1. В задаче рассматривается равновесие системы тел – стрелы и стойки, связанных струной ВС. Прежде чем приступить к определению усилий в стойке и тросах, необходимо найти натяжение струны ВС.
2. В точке С на кран действует вес ![]() груза, масса которого m, следовательно,
груза, масса которого m, следовательно,
G = mg = 2000 × 9,81 = 19600 H = 19,6 кH.
Разложим вес ![]() на две составляющие, действующие вдоль струны ВС и стрелы АС, воспользовавшись правилом треугольника (рис. 49, б). Для этого из произвольной точки K построим вектор
на две составляющие, действующие вдоль струны ВС и стрелы АС, воспользовавшись правилом треугольника (рис. 49, б). Для этого из произвольной точки K построим вектор ![]() а затем из его начала и конца проведем линии, параллельные ВС и АС. В получившемся силовом треугольнике KLM (КL || ВС и LM || CA) сторона KL изображает силу растягивающую струну ВС, а сторона LM – силу
а затем из его начала и конца проведем линии, параллельные ВС и АС. В получившемся силовом треугольнике KLM (КL || ВС и LM || CA) сторона KL изображает силу растягивающую струну ВС, а сторона LM – силу ![]() сжимающую стрелу АС.
сжимающую стрелу АС.
Из построения следует, что 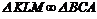 , поэтому Отсюда
, поэтому Отсюда 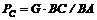 .
.
Неизвестную по условию задачи длину струны ВС легко найти, рассмотрев прямоугольный треугольник BCF (см. рис. 49, а):
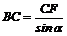 .
.
Таким образом, кН.
3. Перенесем силу вдоль линии ее действия из точки С в точку В и рассмотрим равновесие узла В, на который, кроме нагрузки РС = 45,3 кН, действуют реакции трех связей: ![]() – реакция стойки, и
– реакция стойки, и ![]() – реакции тросов BD и BE. В соответствии с общим правилом считаем, что все связи растянуты (рис. 49, в).
– реакции тросов BD и BE. В соответствии с общим правилом считаем, что все связи растянуты (рис. 49, в).

|
Из за большого объема этот материал размещен на нескольких страницах:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 |




