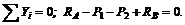
Подставляя в это уравнение числовые значения, получаем тождество
14 – 10 – 20 + 16 = 0 или 0 = 0.
Значит задача решена правильно. Реакции опор: RА = 14 кH и RB = 16 кН.
При решении задач рекомендуется не пренебрегать проверкой. От правильности определения реакций опор зависит правильность всего остального решения или расчета.
Задача 21. На консольную балку, имеющую в точке А шарнирно-неподвижную, а в точке В шарнирно-подвижную опору, действуют две сосредоточенные нагрузки: P1 = 18 кН и Р2 = 50 кH, как показано на рис. 38, а; угол a = 40°. Определить реакции опор балки.
Решение.
1. Рассматривая находящуюся в равновесии балку AD, видим, что в точке С на нее действует вертикально вниз нагрузка ![]() , а в точке D под углом a к АВ действует другая нагрузка
, а в точке D под углом a к АВ действует другая нагрузка ![]() (рис. 38, б).
(рис. 38, б).
2. Освобождаем балку от связей и заменим их действие реакциями. В месте шарнирно-подвижной опоры В возникает вертикальная реакция Направление реакции шарнирно-неподвижной опоры в данном случае непосредственно определить нельзя, поэтому заменим эту реакцию ее двумя составляющими и ![]() .
.
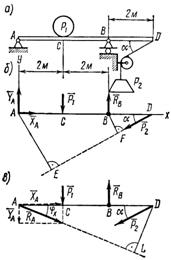
Рис. 38
3. Для полученной системы из пяти сил, произвольно расположенных в плоскости, составим систему уравнений равновесия, расположив ось х вдоль балки, а за центры моментов приняв точки А и В:
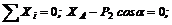 (1)
(1)
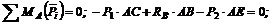 (2)
(2)
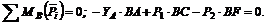 (3)
(3)
4. Решаем полученные уравнения. Из (1)
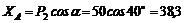 кН.
кН.
Так как АЕ = AD sin a, то из (2)
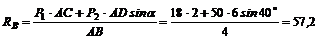 кН.
кН.
Замечая, что BF = BD sin a, из (3) получаем
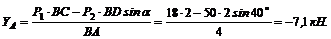
Знак минус, получившийся в последнем случае, показывает, что YА – вертикальная составляющая реакция неподвижного шарнира – направлена вниз, а не вверх, как предполагалось перед составлением уравнения (3).
5. При необходимости реакцию шарнира А легко определить (рис. 38, в).
Модуль реакции шарнира А найдем из формулы
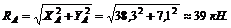
Направление реакции установим, определив угол:
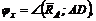
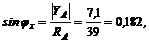
откуда 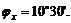
6. Проверим правильность решения задачи. Так как при решении не использовано уравнение проекций на ось у, то используем его для проверки:
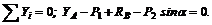
Уравнение составлено по рис. 38, б.
После подстановки в это уравнение известных значений получим:
– 7,1 – 18 + 57,2 – 50 sin 40° = 0;
– 25,1 + 57,2 – 32,1 = 0 и 0 = 0.
В данном случае, проверка решения при помощи уравнения проекций не дает возможности установить правильность определения полной реакции шарнира А. Чтобы проверить и этот этап решения, составим уравнение моментов относительно точки D, воспользовавшись рис. 38, в, на котором изображена реакция так, как она направлена в действительности:
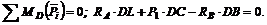
Подставляем в это уравнение числовые значения, имея в виду, что
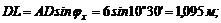
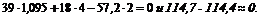
Расхождение в результатах, равное 0,3, получается из-за округлений при вычислениях.
В следующих задачах проверка решения не приводится и ее рекомендуется производить самостоятельно.
Задача 22. Горизонтальная балка имеет в точке А шарнирно-подвижную опору, плоскость которой наклонена к горизонту под углом a = 24° (рис. 39, а), а в точке В – шарнирно-неподвижную опору. Балка нагружена в точках С и D двумя сосредоточенными силами P1 = 24 кН и Р2 = 30 кН. Определить реакции опор.
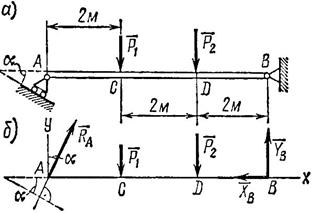
Рис. 39
Решение.
1. Балка нагружена двумя параллельными силами, реакция подвижного шарнира направлена не параллельно вертикальным нагрузкам, а под углом a к вертикали – перпендикулярно к опорной поверхности шарнира (рис. 39, б). Поэтому реакция неподвижного шарнира не будет направлена вертикально, и ее целесообразно заменить двумя составляющими и ![]() .
.
2. Расположив оси х и у, как показано на рис. 39, б, составляем уравнения равновесия:
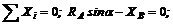 (1)
(1)
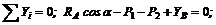 (2)
(2)
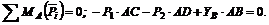 (3)
(3)
3. Решаем полученные уравнения. Из уравнения (3) находим YB:
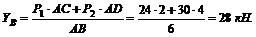
Из уравнения (2) находим RA:
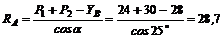 кН.
кН.
Из уравнения (1) находим ХВ:
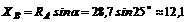 кН.
кН.
Таким образом, реакция шарнира A RA = 28,7 кН, а составляющие реакции шарнира В ХВ = 12,1 кН и YB = 28 кН.
4. Проверку решения производим при помощи уравнения моментов относительно точки С или D.
§ 10. Виды опор балочных систем.
Определение опорных реакций
Балками называют такие элементы конструкций машин, приборов, сооружений, которые в процессе работы воспринимают в основном поперечные относительно оси нагрузки и передают их через опорные устройства другим элементам конструкции или основанию. Примером могут служить такие детали машин, как валы, оси, рычаги, детали строительных конструкций, фермы мостов и т. п.
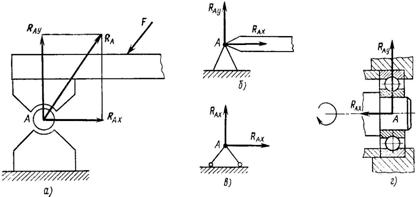
Рис. 40
Конструкции опор балок можно свести к трем видам.
Шарнирно-неподвижная опора препятствует любому поступательному перемещению балки, но дает возможность последней поворачиваться вокруг оси шарнира (рис. 40, а). Реакция приложена в центре шарнира А. Для определения неизвестных модуля и направления реакции RA необходимо ее заменить взаимно перпендикулярными составляющими RAx и RAy. На рис. 40, б и в показаны схематические изображения этой опоры. В качестве примера шарнирно-неподвижной опоры может служить подшипниковый узел (рис. 40, г).
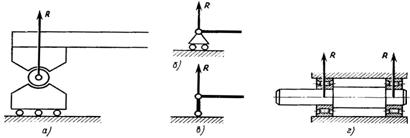
Рис. 41
Шарнирно-подвижная опора – нижняя часть поставлена на катки (рис. 41, а), поэтому такая опора не препятствует небольшому перемещению балки в направлении, параллельном опорной поверхности. Реакция опоры в данном случае приложена в центре шарнира и направлена по нормали к опорной поверхности (трением катков пренебрегаем). Схематическое изображение показано на рис. 41, б и в. На рис. 41, г показана шарнирно-подвижная (плавающая) опора вала.
Жесткая заделка (рис. 42) препятствует любому поступательному движению балки и повороту последней в плоскости действия сил. Поэтому, кроме реакции RA, которую мы раскладываем на RAx и RAy, со стороны заделки к балке приложен еще опорный момент МA – уравновешивающий момент активных сил, стремящихся повернуть балку.
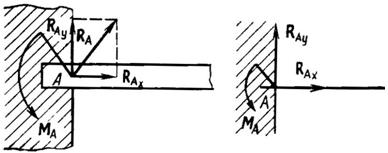
Рис. 42
Задача 23. Определить опорные реакции балки (рис. 43), нагруженной парой М = 4 Нм, и равномерно распределительной по длине l = 0,3 м нагрузкой, интенсивность которой q = 2 Н/м; весом балки пренебрегаем.
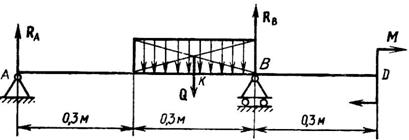
Рис. 43
Решение.
Мысленно освободив балку от связей и заменив их реакциями RA и RB получим уравновешенную систему параллельных сил. Равномерно распределенная нагрузка задана величиной интенсивности и длиной участка, на котором она распределена. Для решения задачи необходимо заменить ее равнодействующей силой Q = ql, приложенной в середине этого участка в точке К.
Для решения составим следующие уравнения равновесия:
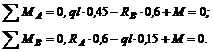
Откуда 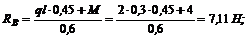
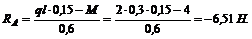
Знак «минус» указывает на то, что реакцию RA нужно направить вниз, а не вверх, как мы сделали предварительно.
Для проверки используем уравнение

|
Из за большого объема этот материал размещен на нескольких страницах:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 |




