При графоаналитическом решении модули сил F1 и F2 определяют по формулам, полученным из выражения (1):
; 
.
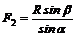Задача 2. Определить силы, растягивающие нити АВ и ВС, которые удерживают груз весом G = 20 Н в равновесии (рис. 6, а).
Решение. Графическое (рис. 6, б): из точки О на плоскости рисунка строим в выбранном масштабе вектор силы G. Из точки О проводим прямые, параллельные нитям ОМ и ON. Затем из конца вектора G проводим прямые KL и КЕ, чтобы получился параллелограмм, у которого стороны OL и ОЕ соответствуют в данном масштабе искомым силам.
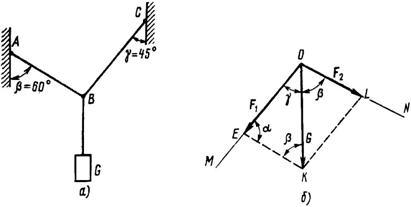
Рис. 6
Графоаналитическое (рис. 6, б): Так как известны все углы в треугольнике ОЕК, а также модуль силы G, можно использовать теорему синусов для определения модулей сил F1 и F2:
,
где 
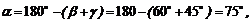откуда
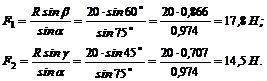
Задача 3. Фонарь весом 80 Н подвешен на кронштейне ABC, укрепленном на вертикальной стене (рис. 7). Определить усилия, возникшие в горизонтальном стержне СВ и наклонной тяге АВ после подвески фонаря, если СВ = 1 м и АВ = 1,2 м. Соединения в точках А, В и С кронштейна – шарнирные.
Решим задачу графоаналитическим методом по правилу параллелограмма.
1. Используя рис. 7, на котором изображен кронштейн, строим параллелограмм сил. Через произвольную точку а (рис. 29) проводим прямые A1A2 и С1С2, параллельные соответственно тяге АВ и стержню СВ (рис. 7).
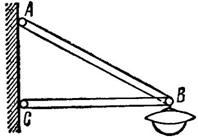
Рис. 7
Из той же точки а откладываем вертикально вниз отрезок ab, который изображает силу 
Из точки b проводим прямые bd || С1С2 и bc || A1A2. В получившемся параллелограмме adbc стороны ad и ас изображают соответственно искомые усилия и 
.
2. Теперь имеются две геометрические фигуры – треугольник ABC (см. рис. 7), изображающий заданный кронштейн, и силовой параллелограмм (рис. 8).
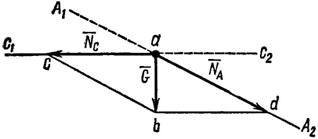
Рис. 8
Геометрически D ABC (рис. 7) и D adb, или, что все равно, D abc
(рис. 8), подобны между собой.
Используя свойство подобных треугольников (замечаем, что db = ac = Nc), получаем
.
3. Решая получившиеся пропорции, находим
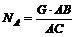и 
.
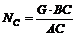Неизвестную в кронштейне длину АС найдем по теореме Пифагора (из условия задачи ясно, что угол АСВ – прямой)
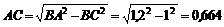м.
Подставляя в выражения для NА и Nc исходные данные, получаем
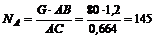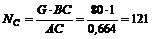H; 
H.
Задача 4. При помощи двух нерастяжимых нитей АС и ВС удерживается груз, вес которого 12 Н. Положение нитей и груза показано на рис. 9. Определить натяжения нитей.
Решим задачу графоаналитическим методом по правилу треугольника с использованием тригонометрических соотношений.
1. Прежде всего необходимо силу G = =12 Н разложить на две составляющие, линии действия которых совпадают с направлениями линий АС и ВС.
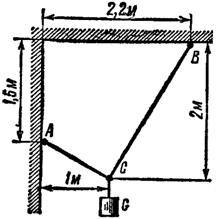
Рис. 9
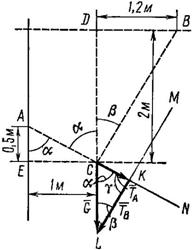
Рис. 10
2. Изобразим силу 
отрезком (рис. 10). Затем проведем из точки С прямую CN, продолжив АС, а из точки L – прямую LM параллельно положению нити ВС. Получим силовой треугольник CKL, в котором стороны СK и KL изображают искомые силы натяжения нитей АС и ВС.
3. Если в треугольнике CKL известны углы a, b и g, то задачу легко решить по теореме синусов:
.
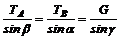4. Из построения силового треугольника следует, что
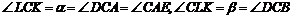
(для наглядности положение нитей относительно вектора G показано на рис. 10 штриховой линией). А так как треугольники D АСЕ и D BCD – прямоугольные, то из D ACE
Из D ВСD
Угол g легко найдем как дополнение к Ð 180°:
.
5. И теперь, зная углы a, b и g, из уравнения (1)
Н
и
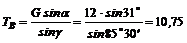Н.
Таким образом, нить CA растягивается усилием, равным 6,25 Н, а нить СВ – усилием 10,75 Н.
§ 3. Сложение плоской системы сходящихся сил.
Силовой многоугольник
Равнодействующую плоскость системы сходящихся сил можно найти графически с помощью построения силового многоугольника.
Пусть дана система сил F1, F2, F3, F4 (рис. 11, a). Выберем на плоскости чертежа произвольную точку O (рис. 11, б). Из нее проводим в выбранном масштабе вектор, равный по модулю и параллельный силе f1. Из конца этого вектора проводим вектор, равный силе F2. Из конца вектора силы F2 строим вектор, равный и параллельный силе F3, и т. д. Соединив точку О с концом последнего вектора, получим замыкающую сторону многоугольника ON, которая в данном масштабе представляет собой искомую равнодействующую системы – R. Действительно, диагональ силового многоугольника OL равна вектору R1, который является геометрической суммой векторов F1 и F2: R1= F1+ F2 . Вторая диагональ ОМ равна R2= R1+ F3= F1+ F2+ F3. Очевидно, что замыкающая сторона R = R2 + R4 = F1 + F2 + F3 + F4 есть равнодействующая системы, равная геометрической сумме всех заданных сил. Точка приложения равнодействующей совпадает с точкой А.
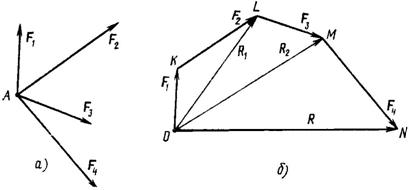
Рис. 11
Модуль и направление равнодействующей не изменятся, если изменить порядок, в котором откладываются векторы сил при построении силового многоугольника.
Следствие. Если система сил является уравновешенной, то равнодействующая системы равна нулю (R = 0). В этом случае силовой многоугольник замкнут, т. е. конец последнего вектора должен совпадать с началом первого.
Замкнутость силового многоугольника является геометрическим условием равновесия плоской системы сходящихся сил. Это условие используют при решении задач на равновесие.
Задача 5. Шар весом G = 20 Н (рис. 12, а) подвешен к вертикальной стене при помощи нити СВ. Определить натяжение нити и силу давления шара на стену, если угол между стеной и нитью a = 30°.
Решение.
1. Рассмотрим равновесие шара под действием трех сил: силы тяжести G, реакции нити RC и реакции стены RA. Линии действия всех сил пересекаются в центре шара 0.
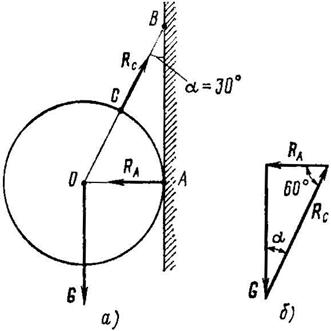
Рис. 12
2. Строим замкнутый силовой треугольник, начиная с известного вектора G (рис. 12, б). Модули неизвестных сил RA и RC, равные соответственно давлению шара на стену и натяжению нити, определим из полученного треугольника:
,
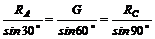откуда
.
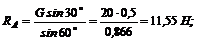
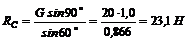Задача 6. Определить равнодействующую четырех сил: P1=18 Н, Р2 = 10 Н, Р3 = 6 Н и Р4 = 8 Н, приложенных к одной точке А и направленных, как показано на рис. 13.
Решение – методом проекций на координатные оси.
1. Изображаем на рисунке четыре данные силы и выбираем расположение осей проекций. В данном случае удобно начало осей поместить в точке А, а оси совместить с силами и 
(рис. 13, а).
|
Из за большого объема этот материал размещен на нескольких страницах:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 |
