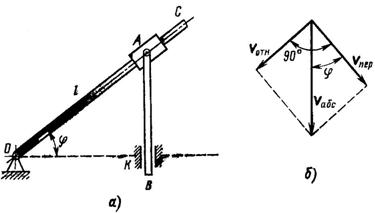
Рис. 75
Решение.
1. Движение точки А вместе со стержнем АВ относительно неподвижных направляющих К можно считать сложным, складывающимся из двух движений:
относительного поступательного вдоль кулисы ОС; вектор относительной скорости voth направлен вдоль кулисы (рис. 75, б);
переносного вращательного вместе с кулисой ОС; вектор Vпep направлен перпендикулярно кулисе ОС и его модуль
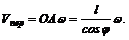
2. Скорость абсолютного движения точки А направлена по вертикали.
3. Из параллелограмма скоростей (рис. 75, б) очевидно, что модуль относительной скорости точки А:
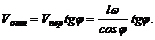
Задача 49. Вниз по течению реки равномерно плывет лодка, приводимая в движение гребным винтом от мотора. Скорость течения реки 4 км/ч, скорость лодки, сообщаемая ей гребным винтом по отношению к воде, составляет 8 км/ч. Определить скорость лодки относительно берегов и расстояние, которое проходит лодка вдоль берегов за 20 мин.
Решение иллюстрировать рисунком, считая берега реки на данном участке прямолинейными и параллельными.
Решение.
1. Лодку принимаем за материальную точку, а водную массу реки – за материальную среду.
Движение лодки относительно берегов или, иначе говоря, движение лодки, наблюдаемое с берега, – это абсолютное движение. Переносное движение лодки – ее перемещение вместе с рекой; скорость VP = 4 км/ч, которую сообщает лодке река, – ее переносная скорость.
Относительное движение – перемещение лодки по поверхности воды, создаваемое гребным винтом; скорость относительного движения Vл=8 км/ч.
2. Так как в данном случае переносное и относительное движения направлены в одну и ту же сторону, то скорость лодки относительно берегов (абсолютная скорость):
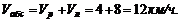
3. За время 
лодка вдоль берегов проходит расстояние:
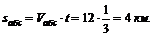
4. Иллюстрируем решение задачи следующим образом (рис. 76).
Изобразим на рисунке тот участок водного пространства, который проходит лодка независимо от того, перемещается этот участок воды или нет. За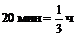 
лодка успевает пройти по этому пространству из положения L0 в положение L1 расстояние
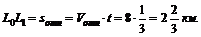
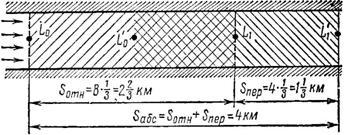
Рис. 76
За эти же 20 мин, или 
, показанное водное пространство переместится на расстояние
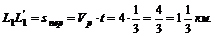
Таким образом, лодка, находившаяся в начале рассматриваемого движения относительно берегов в точке L0, через 20 мин оказывается в точке т. е. проходит расстояние
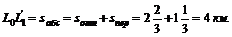
Следовательно, скорость абсолютного движения
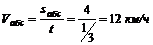
Задача 50. Два автомобиля 1 и 2 движутся параллельно друг другу в одну и ту же сторону со скоростями V1 = 80 км/ч и V2 = 60 км/ч (рис. 77, а). С какой скоростью второй автомобиль двигается относительно первого?
Решение.
1. Ответ «по соображению» получается мгновенно: V2-1 = 60 – 80 =
= – 20 км/ч, т. е. относительно первого второй автомобиль двигается со скоростью 20 км/ч, но в обратную сторону.
2. Объясним это решение с точки зрения теории сложного движения точки. Условно остановим первый автомобиль. Но тогда, чтобы не изменились условия движения, необходимо мысленно представить, что полотно дороги под вторым автомобилем и вместе с ним получает движение в обратную сторону со скоростью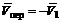 
(рис. 77, б).
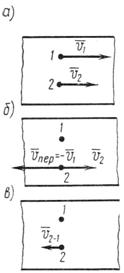
Рис. 77
Находясь в условном переносном движении со скоростью Vпер, второй автомобиль относительно дороги движется со скоростью V2.
Поэтому результирующая обеих скоростей численно равна их разности:
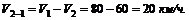
Как видно на рис. 77, в, результирующая направлена в сторону, противоположную скорости 
.
Задача 51. Расстояние S = 90 км между двумя пристанями, расположенными на реке (рис. 78), теплоход проходит без остановки в одном направлении (по течению) за t1 = 3 ч и в обратном направлении (против течения) за t2 = 5 ч. Определить скорость течения реки и собственную скорость теплохода.
Решение.
1. Теплоход, который принимаем за материальную точку, двигаясь по течению, имеет абсолютную скорость (скорость относительно берегов):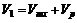 
, где Vтх – искомая собственная скорость теплохода (относительная скорость); Vр – скорость течения реки (переносная скорость).
При движении против течения абсолютная скорость теплохода
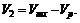
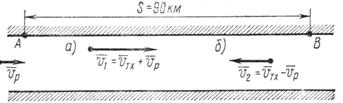
Рис. 78
2. Движение теплохода по течению описывается уравнением (рис. 78, а)
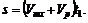
Движение теплохода против течения происходит по уравнению (рис. 78, б)
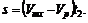
3. Решаем полученную систему уравнений:
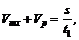
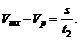
Сложим правые и левые части этих уравнений:
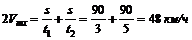
и
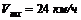
Вычитаем из верхнего равенства нижнее:
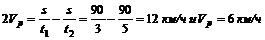
Таким образом, собственная скорость теплохода составляет 24 км/ч и скорость течения реки равна 6 км/ч.
Задача 52. От одного берега реки к другому плывет лодка, держа курс перпендикулярно к берегам (рис.79). Ширина реки 800 м. Лодка достигает противоположного берега через 12 мин после начала переправы. За это время лодку сносит вниз по течению на расстояние 600 м. Определить скорость течения реки; собственную скорость лодки:
скорость лодки относительно берегов. Скорость течения у берегов и на середине реки считать одинаковой.
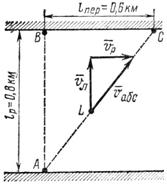
Рис. 79
Решение.
1. Изобразим на рисунке движение лодки (рис. 79). Представим, что лодка отплывает из точки А на правом берегу. Если бы не было течения, она достигла бы противоположного берега в точке В; известно, что ширина реки АВ = lр = 800 м = 0,8 км. Но лодку сносит вниз по течению (переносное движение) на расстояние ВС = lпер = 600 м = 0,6 км и поэтому движение лодки относительно берегов (абсолютное движение) происходит по прямой АС.
Обозначим точкой L положение лодки через некоторое время после начала движения. Скорость лодки относительно берегов – абсолютная скорость 
– направлена вдоль прямой АС и складывается из собственной скорости 
, сообщаемой гребным винтом или веслами, и из переносной скорости течения реки
2. Допустим, что нет течения реки, тогда лодка будет перемещаться относительно берегов так же, как и относительно воды, по прямой АВ, и ее движение опишется уравнением
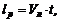
где t – время переправы (t = 12 мин = 0,2 ч). Отсюда находим собственную скорость лодки (скорость лодки относительно воды – относительную скорость):
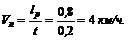
3. Если лодка будет плыть, подчиняясь только течению реки, ее движение опишется уравнением
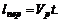
Из этого уравнения найдем скорость течения реки:
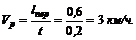
4. Теперь из прямоугольного треугольника скоростей (см. рис. 79) легко найти скорость лодки относительно берегов – абсолютную скорость:
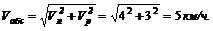
Задача 53. В кривошипно-кулисном механизме с поступательно движущейся кулисой ВС кривошип ОА (расположенный позади кулисы) длиной l = 400 мм вращается с постоянной угловой скоростью w = 10 рад/с. Концом А, соединенным шарнирно с камнем, скользящим в прорези кулисы, кривошип сообщает кулисе ВС возвратно-поступательное движение. Определить скорость кулисы в момент, когда кривошип образует с осью кулисы угол х ОА = 30° (рис. 80, а).
|
Из за большого объема этот материал размещен на нескольких страницах:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 |
