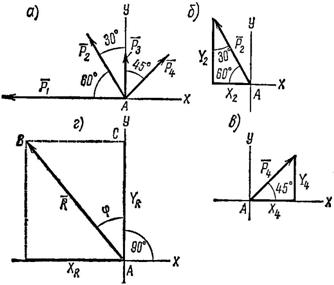
Рис. 13
2. Находим проекции данных сил на ось х (рис. 13,б):
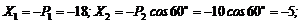

3. Находим проекции данных сил на ось у (рис. 13,в):
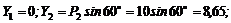
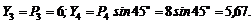
4. Находим проекции искомой равнодействующей на оси х и у:
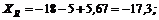
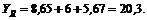
Проекция на ось х получается отрицательной, а на ось у положительной. Значит вектор ![]() заменяющий действие четырех данных сил и приложенный к точке А, должен быть направлен относительно оси у вверх, а относительно оси х – влево. Положение равнодействующей R показано отдельно на рис. 13, г.
заменяющий действие четырех данных сил и приложенный к точке А, должен быть направлен относительно оси у вверх, а относительно оси х – влево. Положение равнодействующей R показано отдельно на рис. 13, г.
5. Находим модуль равнодействующей:
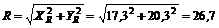 Н.
Н.
6. Находим угол j, определяющий направление R относительно оси у (см. рис. 13, а):
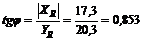
и, следовательно, ![]() .
.
Для определения угла j использован D ABC (см. рис. 13, г), в котором 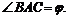 Поэтому XR не имеет значения и в выражение tgj подставлена его абсолютная величина.
Поэтому XR не имеет значения и в выражение tgj подставлена его абсолютная величина.
Угол j можно найти при помощи синуса:
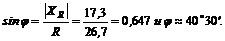
Таким образом, равнодействующая четырех заданных сил равна 26,7 Н, направлена под углом 40°30' к положительному направлению оси у и под углом 90° + 40°30' = 130°30' к положительному направлению оси х.
Задача 7. К концу В веревки АВ прикреплено кольцо, на которое действуют четыре силы: Р1 = 40 H, Р2 = 25 H, P3 = 25 H и P4 = 20 H, направленные, как показано на рис. 14, а (сила Р2 горизонтальна). Определить усилие, возникшее в веревке, и ее направление относительно горизонтали.
Решение – методом проекций.
1. Веревка будет натянута равнодействующей четырех заданных сил. Следовательно, определив модуль равнодействующей, получим усилие, возникшее в веревке, а определив направление равнодействующей, найдем положение натянутой веревки.
2. Изобразим точку В с действующими на нее силами на отдельном рисунке (рис. 14, б) и совместим оси проекций с силами ![]() и
и ![]() .
.
3. Найдем проекции заданных сил на ось х:
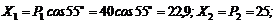
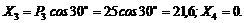
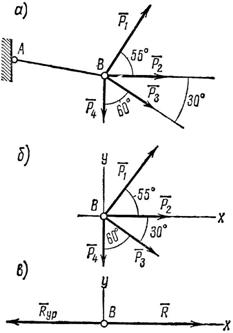
Рис. 14
4. Найдем проекции заданных сил на ось у:
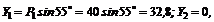
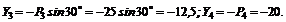
5. Найдем проекции равнодействующей на оси х и у:
![]()
![]()
6. Найдем модуль равнодействующей:
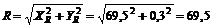 H.
H.
Как видно, в данном случае проекция равнодействующей на ось у очень мала по сравнению с проекцией на ось х. Поэтому равнодействующая практически численно равна проекции на ось х. Следовательно, можно принять, что вектор равнодействующей направлен вдоль оси х вправо (проекция на ось х положительна), т. е. горизонтально.
Таким образом, четыре заданные силы натягивают веревку равнодействующей силой R, приложенной к точке В (к кольцу на конце веревки) и направленной горизонтально.
Другой конец веревки (точка А, рис. 14, а) закреплен, поэтому на кольцо В со стороны веревки действует еще одна сила, численно равная равнодействующей, но направленная в противоположную сторону. Эта сила называется уравновешивающей системы четырех сил.
На рис. 14, в показаны равнодействующая R и уравновешивающая ![]() .
.
Задача 8. На конце В горизонтального стержня АВ необходимо прикрепить две нити с грузами Р1 = 4 кH и Р2 = 0,8 кH, как показано на рис. 15, а. Под каким углом к этому стержню следует присоединить второй стержень ВС, чтобы стержень АВ растягивался силой РА = 2 кН. Какое усилие при этом будет испытывать стержень ВС?
Соединения стержней между собой и с опорами шарнирные.
Решение – методом проекций.
1. На точку В действуют три силы: – вертикально вниз, ![]() – вдоль нити от точки В к блоку (под углом 30° к горизонтали) и противодействие (реакция) стержня тому растягивающему действию, которое испытывает стержень. Изобразим эти три силы на рис. 15, б и найдем их равнодействующую, вдоль направления которой необходимо установить стержень ВС.
– вдоль нити от точки В к блоку (под углом 30° к горизонтали) и противодействие (реакция) стержня тому растягивающему действию, которое испытывает стержень. Изобразим эти три силы на рис. 15, б и найдем их равнодействующую, вдоль направления которой необходимо установить стержень ВС.
2. Оси проекций совместим с силами и ![]() и определим проекции искомой равнодействующей сначала на ось х, а потом на ось у, зная, что каждая из них равна алгебраической сумме проекций данных сил на соответствующую ось:
и определим проекции искомой равнодействующей сначала на ось х, а потом на ось у, зная, что каждая из них равна алгебраической сумме проекций данных сил на соответствующую ось:
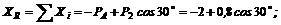
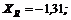
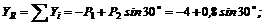
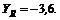
3. Обе проекции получаются отрицательными. Значит, равнодействующая расположится так, как показано штриховым на рис. 15, б, и положение стержня ВС определится углом 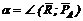 .
.
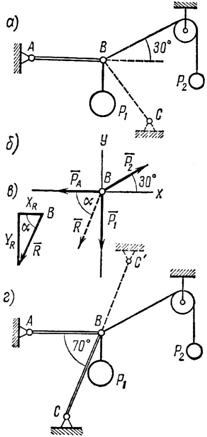
Рис. 15
4. Определим значение угла a из треугольника, образуемого и его проекциями (рис. 15, в):
![]() ,
, ![]()
5. Стержень ВС необходимо установить под 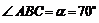 к стержню АВ, и тогда он будет сжиматься силой, равной
к стержню АВ, и тогда он будет сжиматься силой, равной
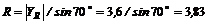 кН.
кН.
Описанное положение стержня показано на рис. 15, г.
Если же установить стержень, как показано на рисунке штриховой линией ВС, то стержень будет испытывать растяжение, равное той же силе R = 3,83 кН.
Задача 9. Определить равнодействующую пяти сил:
Р1 = 52 Н, Р2 = 70 Н, Р3 = 69 Н, Р4 = 77 Н, Р5 = 70 Н, действующих на точку А, как показано на рис. 16, а.
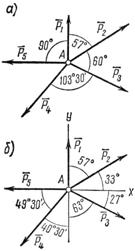
Рис. 16
Решение – методом проекций.
1. Так как силы и направлены друг к другу под прямым углом, то и совместим с этими силами ось проекций. Тогда векторы ![]() ,
, ![]() и будут образовывать с осями проекций углы, показанные на рис. 16, б.
и будут образовывать с осями проекций углы, показанные на рис. 16, б.
2. Найдем проекцию равнодействующей на ось х:
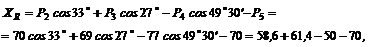
![]()
3. Найдем проекцию равнодействующей на ось у:
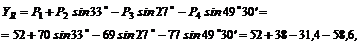
![]()
4. Обе проекции искомой равнодействующей равны нулю, значит и сама равнодействующая также равна нулю.
Таким образом, данная система сил уравновешена. Иными словами, любую из пяти заданных сил можно рассматривать как уравновешивающую четыре остальных.
§ 4. Проекция силы на ось.
Проекция силы на две взаимно-перпендикулярные оси координат
Кроме рассмотренных выше графического и графоаналитического методов решения задач, в статике широко распространен аналитический метод их решения, или метод проекций.
Проекцией силы на ось (рис. 17) является отрезок оси, заключенный между проекциями на эту ось начала и конца вектора силы. Проекцию обычно обозначают той же буквой, что и силу, но с индексом. Например, Fx – проекция силы F на ось х.

|
Из за большого объема этот материал размещен на нескольких страницах:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 |




