Требуется при данных совокупных издержках определить такое количество факторов производства, которые максимизируют объем продукции z.
Математическая модель этой задачи имеет вид: определить такие переменные x1 и x2, удовлетворяющие условиям
![]() ,
,
x![]()
![]() , x
, x![]()
![]() , (3)
, (3)
при которых функция
![]() (4)
(4)
достигает максимума.
Как правило, функция (4) может иметь произвольный нелинейный вид.
Используя классические методы оптимизации, следует четко представлять различия между локальным экстремумом функции, глобальным экстремумом и условным экстремумом. При этом полезно повторить определение локального и глобального экстремумов для функций одной переменной. Понятие условного экстремума вводится для случая, когда число переменных n не меньше двух (![]() ).
).
Будем предполагать, что функция ![]()
![]() дважды дифференцируема в точке
дважды дифференцируема в точке![]() , (
, (![]() ) и в некоторой ее окрестности. Если для всех точек этой окрестности
) и в некоторой ее окрестности. Если для всех точек этой окрестности ![]() или
или ![]() , то говорят, что функция
, то говорят, что функция ![]() имеет экстремум в
имеет экстремум в ![]() (соответственно максимум или минимум).
(соответственно максимум или минимум).
Точка ![]() , в которой все частные производные функции
, в которой все частные производные функции ![]() равны 0, называется стационарной точкой.
равны 0, называется стационарной точкой.
Необходимое условие экстремума. Если в точке ![]() функция
функция ![]() имеет экстремум, то частные производные функции в этой точке равны нулю:
имеет экстремум, то частные производные функции в этой точке равны нулю:
![]()
![]()
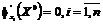 .
.
Следовательно, точки экстремума функции ![]() удовлетворяют системе уравнений:
удовлетворяют системе уравнений:
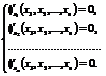 (5)
(5)
Как и в случае одной переменной, необходимое условие не является достаточным для того, чтобы стационарная точка была точкой экстремума. Для получения достаточных условий следует определить в стационарной точке знак дифференциала второго порядка. Дифференциал второго порядка обозначается ![]() и равен сумме произведений частных производных второго порядка на соответствующие приращения аргументов. Если от частной производной
и равен сумме произведений частных производных второго порядка на соответствующие приращения аргументов. Если от частной производной ![]() найти частную производную по переменной xj, то получим частную производную второго порядка по переменным x
найти частную производную по переменной xj, то получим частную производную второго порядка по переменным x![]() и x
и x![]() , которая обозначается
, которая обозначается ![]() .
.
В этом случае ![]() .
.
Достаточные условия экстремума.
а) в стационарной точке ![]() функция
функция ![]() имеет максимум, если
имеет максимум, если ![]() , и минимум, если
, и минимум, если![]() при любых Dxi и Dxj, не обращающихся в нуль одновременно;
при любых Dxi и Dxj, не обращающихся в нуль одновременно;
б) если ![]() может принимать в зависимости от Dxi и Dxj, и положительные, и отрицательные значения, то в точке
может принимать в зависимости от Dxi и Dxj, и положительные, и отрицательные значения, то в точке ![]() экстремума нет;
экстремума нет;
в) если ![]() может обращаться в нуль не только при нулевых приращениях Dxi и Dxj , то вопрос об экстремуме остается открытым.
может обращаться в нуль не только при нулевых приращениях Dxi и Dxj , то вопрос об экстремуме остается открытым.
Для функции двух переменных![]() достаточные условия еще не очень сложны. Существует четыре частные производные второго порядка:
достаточные условия еще не очень сложны. Существует четыре частные производные второго порядка:
![]()
![]() ,
, ![]() ,
,![]() .
.
Из них две смешанные: ![]() ,
, ![]() , если непрерывны, то равны.
, если непрерывны, то равны.
Найдем значения частных производных второго порядка в стационарной точке 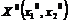 :
:
![]() ;
; ![]() ;
;
![]() ;
; ![]() .
.
(можно убедиться, что ![]() ). Обозначим через D определитель, составленный из
). Обозначим через D определитель, составленный из ![]() для
для ![]()
![]()
Тогда достаточные условия экстремума функции двух переменных имеют вид:
а) если ![]() и
и ![]() (
(![]() ), то в точке
), то в точке ![]() функция имеет максимум; если
функция имеет максимум; если ![]() и
и ![]() (
(![]() ), то в точке
), то в точке![]() минимум;
минимум;
б) если ![]() , то экстремума нет;
, то экстремума нет;
в) если ![]() , то вопрос об экстремуме остается открытым.
, то вопрос об экстремуме остается открытым.
Схема определения экстремума функции n переменных совпадает с правилами определения локального экстремума функции одной переменной.
Задача 1. Исследовать на экстремум функцию 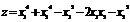 .
.
Решение. Находим частные производные:
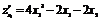
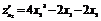 . (6)
. (6)
Приравниваем частные производные к нулю:
![]()
![]() (7)
(7)
Решаем систему (7). Вычитая из 1-го уравнение 2-ое, получим 4x![]() -4x
-4x![]()
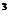 =0
=0![]() , поэтому x
, поэтому x![]() =x
=x![]() и из 1-го уравнения получаем x
и из 1-го уравнения получаем x![]()
![]() -x
-x![]() =0, откуда: x
=0, откуда: x![]() =0 или x
=0 или x![]() =
=![]() 1.
1.

|
Из за большого объема этот материал размещен на нескольких страницах:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 |
 Основные порталы (построено редакторами)
Основные порталы (построено редакторами)

